| Titel: | Ueber einen neuen Gegenlenker von Hrn. Sarrat. |
| Fundstelle: | Band 129, Jahrgang 1853, Nr. LXXII., S. 329 |
| Download: | XML |
LXXII.
Ueber einen neuen Gegenlenker von Hrn. Sarrat.
Nach den Comptes rendus, Juni 1853, Nr. 24 und
26.
Mit Abbildungen auf Tab.
VI.
Ueber Sarrat's Gegenlenker.
Wenn man aus fünf unveränderlichen Gliedern A, B, C, D, E
in der Art ein veränderliches System construirt, daß man sie je zwei durch eine
gemeinschaftliche bewegliche Achse, um welche beide ohne zu gleiten sich drehen
können, verbindet, und sich die beiden äußern Glieder A
und E um feste Achsen drehen läßt, so kann man dem
mittleren Gliede C dadurch eine genaue geradlinige
Bewegung sichern, daß man sich durch die Richtung dieser geradlinigen Bewegung zwei
Ebenen, am einfachsten senkrecht zu einander, gelegt denkt, und eine der festen
Achsen zuzn der einen, die andere zu der zweiten Ebene senkrecht legt, und die
Verbindungsachsen der Glieder A und B, B und C mit der ersten,
die Verbindungsachsen der Glieder C und D, D und E mit der zweiten
festen Achse parallel richtet. Das mittlere Glied C,
welches auf diese Weise zwei unter sich rechtwinklige Achsen erhält, muß dann sowohl
in der einen als in der andern jener beiden Ebenen bleiben und sich demnach in der
Durchschnittslinie derselben bewegen.
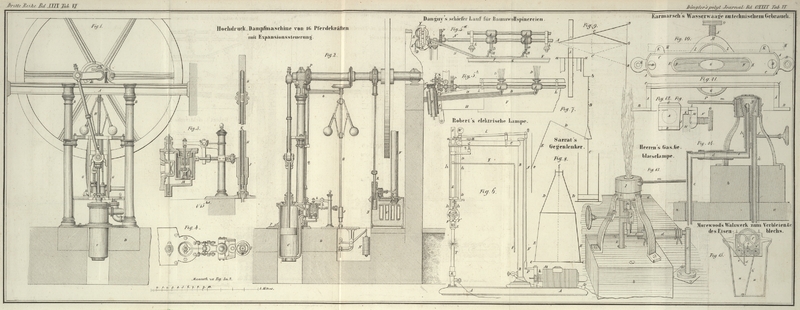
Ein solches System ist z.B. das Schwungrad A, Fig. 7, welches
sich um die feste Achse a, a bewegt, mit der Kurbel a, b, der Bleuelstange B,
der Kolbenstange C einer Pumpe oder einer Dampfmaschine,
und den beiden Gliedern D und E des Gegenlenkers Fig. 7 und 8, von denen das letztere
wieder um eine feste Achse e, e beweglich ist. Man wird
sich mittelst der Skizze Fig. 7 leicht überzeugen,
daß der Kopf der Kolbenstange C sich in einer verticalen
Geraden bewegen muß, wenn die festen Achsen a und e horizontal und senkrecht zu einander sind (geometrisch
genügt es, daß sie beide horizontal und nicht parallel
sind), und wenn die Verbindungsachsen von A und B (die Krummzapfen-Warze b) und von B und C
zu der festen Achse a, die Verbindungsachsen von C und D, D und E dagegen zu der festen Achse e parallel bleiben.
Ueber dieses neue Princip für die Umwandlung einer abwechselnden geradlinigen
Bewegung in eine Kreisbewegung und umgekehrt, spricht sich der Bericht der von der
französischen Akademie ernannten Commission folgendermaßen aus:
„Man kennt von dieser Aufgabe der Bewegungslehre eine große Anzahl,
mitunter sehr alter Auflösungen, unter welchen sich auch das gegliederte
Parallelogramm befindet, welches Watt an dem
Balancier seiner Dampfmaschinen angebracht hat. Man weiß indessen, daß auch
diese letztere Construction, wie andere ähnliche, nicht streng genau ist, daß
vielmehr der Kopf der Kolbenstange immer noch geringe Ablenkungen von der
geometrischen Achse des Dampfcylinders erleidet, welche, wenn auch nur wenig
wahrnehmbar, doch auf den Gang großer Maschinen einen störenden Einfluß äußern,
den selbst die mathematischen Untersuchungen von Prony,
Vincent, Willis u.a. nicht zu beseitigen vermochten. Man weiß auch, daß
diese Uebelstände in der letzten Zeit sowohl in Frankreich, als in England, die
Erfindung anderer, nicht weniger beachtenswerthen Constructionen, aber von einer
ganz andern Natur, veranlaßen, durch welche eine wechselnde geradlinige Bewegung
ohne Anwendung des Balancier in eine fortgehende Kreisbewegung umgewandelt wird.
Wie groß aber auch die Vortheile dieser Constructionen für die Vereinfachung der
großen Maschinen seyn mögen, so ist es nicht weniger wahr, daß in dem alten
System noch eine wahre mathematische, von den Uebelständen der bisherigen
Constructionen freie Auflösung zu finden war, und gerade dieß ist die
wesentliche Eigenschaft der von Hrn. Sarrat vorgelegten Construction.“
„Das Princip dieser Umwandlung ist sehr allgemein und einfach, und
begreift als besondern Fall den der oscillirenden Cylinder. Man sieht ein, daß
diese Auflösung, auf ein System von entsprechender Gliederung ausgedehnt, wie es
der Erfinder schon bemerkt hat, ein Mittel darbieten kann, um den leitenden
Punkt eines Maschinentheiles eine krumme Linie beschreiben zu machen, dadurch
daß man diese Linie als den Durchschnitt zweier leichter zu erhaltenden krummen
Flächen betrachtet.“
Ohne das Verdienst des Hrn. Sarrat schmälern zu wollen, erlauben wir uns diesem Berichte die
Bemerkung beizufügen, daß sich bereits in Hülsse's Maschinen-Encyklopädie eine streng mathematische Auflösung des fraglichen
Problems angegeben findet. Diese gründet sich auf den bekannten Satz der
analytischen Geometrie, daß der Mittelpunkt einer Geraden, deren Endpunkte auf den
beiden Schenkeln eines rechten Winkels gleiten, einen Kreisbogen beschreibt, welcher
den Scheitel des rechten Winkels zum Mittelpunkt hat; denn daraus folgt umgekehrt,
daß wenn der Mittelpunkt C einer Geraden AB, Fig. 9, in einem
Kreisbogen CC, und der eine Endpunkt A derselben in einer durch den Mittelpunkt O dieses Bogens gelegten horizontalen Geraden AO geführt wird, der andere Endpunkt B sich in einer durch denselben Mittelpunkt O gehenden verticalen Geraden BB bewegen muß.
G. D.
Tafeln