| Titel: | Die Scheutz'sche Rechenmaschine; von Dr. H. Meidinger. |
| Autor: | Heinrich Meidinger [GND] |
| Fundstelle: | Band 156, Jahrgang 1860, Nr. LXXXIII., S. 321 |
| Download: | XML |
LXXXIII.
Die Scheutz'sche
Rechenmaschine; von Dr. H.
Meidinger.
(Schluß von S. 256 des vorhergehenden
Heftes.)
Mit einer Abbildung auf Tab. V.
Meidinger, über die Rechenmaschine von Georg und Ed. Scheutz in
Stockholm.
In die Art und Weise, wie die beschriebenen Vorgänge durch Bewegungsmechanismen in
der Maschine ausgeführt werden, können wir hier nicht näher eingehen. Zeichnungen
sind darüber noch gar keine veröffentlicht, und nur über Babbage's Maschine sind einige allgemeine Bemerkungen und Andeutungen im
Edinburgh Review gegeben. Da diese Maschine jedoch
nicht vollendet wurde, so dürfte es auch kein allgemeineres Interesse haben, dieses
Wenige ohne bildliche Darstellung mitzutheilen. Die Maschine von Scheutz ist bis jetzt in ihren Details noch ganz
unbekannt. Zwei bemerkenswerthe Unterschiede lassen sich jedoch in beiden Maschinen
charakterisiren. Die erstere Maschine sollte die ungeheuren Dimensionen von 10 Fuß
hoch, 10 Fuß breit und 5 Fuß tief schließlich erreichen; sie sollte sechs Reihen von
Differenzen erhalten und ihre Rechnungen bis auf achtzehn Ziffern ausdehnen, so daß
sie im Ganzen siebenmal achtzehn oder 126 Zifferringe bekommen hätte. Sie wurde
jedoch mit dem ungeheuren Aufwand an Mitteln thatsächlich bloß bis auf fünf Ziffern
und zwei Differenzenreihen gebracht. Die Zahlen der Tabelle und der Differenzen
befinden sich nicht in einer Horizontalreihe, wie wir in den obigen Figuren
vorausgesetzt, und wie es ohne Zweifel am zweckmäßigsten in der Maschine von Scheutz ausgeführt wurde, sondern sie verlaufen vertical,
so daß man die Zahlen von Oben nach Unten ablesen und ebenso die Differenzen
einsetzen muß. Dadurch hätte natürlich die Maschine, wenn vollendet, die ganz
erstaunlichen Dimensionen in die Höhe bekommen müssen. Die Maschine von Scheutz ist dagegen weit kleiner; sie besitzt bloß die
Größe eines Tafelpianos; sie rechnet bis auf 15 Ziffern, die, wie oben bemerkt, in
der Horizontalreihe stehen, und besitzt vier Ordnungen von Differenzen, weil man
diese Anzahl für alle praktischen Fälle für ausreichend gefunden hat. Sie hat somit
im Ganzen 75 Zifferringe.
Es ist bis jetzt eine Seite der Rechenmaschine nur mehr im Vorübergehen angedeutet
worden, die jedoch derselben ohne Zweifel ihre ganze praktische Bedeutung erst
gegeben hat, nämlich der Druckapparat, in welchem die in der obersten Tabelle
angezeigten Resultate gleich für den Druck stereotypirt werden. Dadurch ist denn
allen Irrthümern vorgebeugt, die während des Setzens vorkommen können und die
mühsame Correctur ist umgangen. In der Maschine von Scheutz sind es acht Ziffern, welche neben einander gedruckt werden können
– eine für das Bedürfniß ausreichende Zahl.
Ist die neunte Decimale größer wie 5, so muß in den gedruckten Tafeln die erste
Decimale um eine Einheit vermehrt werden. Man erreicht dieß in der Maschine auf eine
sehr einfache Weise dadurch, daß man beim Beginn der Rechnung die neunte
Decimalstelle der obersten Reihe schon um 5 vermehrt. Soll eine geringere Zahl von
Zifferstellen, z.B. bloß fünf gedruckt werden, so wird man in diesem Falle die
sechste von Anfang an um 5 vergrößern.
Die von der Maschine berechneten Zahlen der Tabelle werden, sobald sie am Ende einer
halben Umdrehung der Kurbel erhalten sind, während der nächsten halben Umdrehung auf
der Rückseite der Maschine durch Stahlstanzen in eine Bleiplatte in beliebiger Tabellenform eingepreßt, und von
dieser Matrize alsdann auf galvanoplastischem oder anderem Wege eine gewünschte
Anzahl von Druckplatten abgezogen. Diese Operation steht mit dem eigentlich
rechnenden Theil der Maschine in keinem weiteren Zusammenhang, sie wird bloß unter
dem Einfluß der obersten Horizontalreihe von Zifferringen vermittelt; wie dieselbe
ausgeführt wird, darüber vermögen wir eben so wenig wie über die
Rechnungsmaschinerie eine Auskunft zu ertheilen; die beigefügte perspektivische
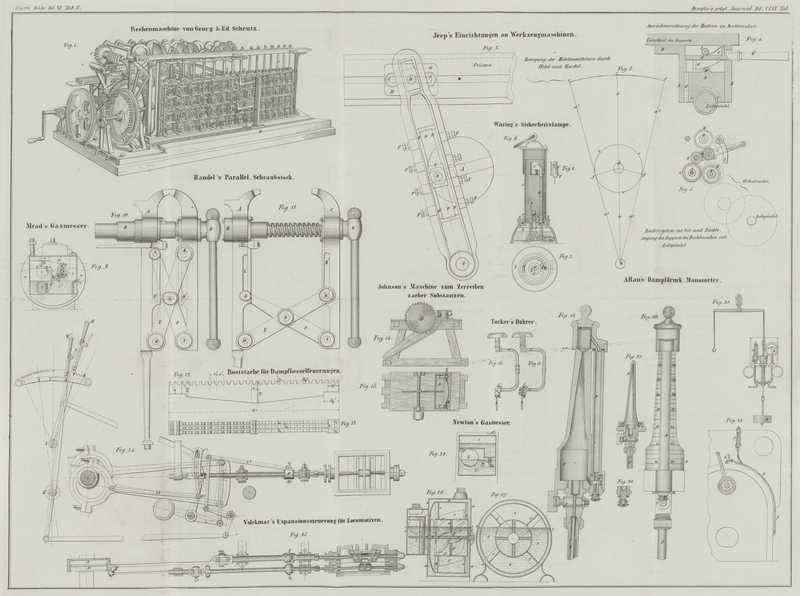
Zeichnung (Tab. V, Fig. 1) kann bloß einen allgemeinen Ueberblick über die ganze Maschine
gewähren. In der Maschine von Babbage hatten für das
Stereotypiren der Tafeln noch keine Vorbereitungen getroffen werden.
In einem Punkt ist noch die vollendete Scheutz'sche
Maschine, so viel bekannt, über das Project der ursprünglichen Maschine mit Glück
hinausgegangen. Sie vermag nämlich eben sowohl fünfzehn dem Decimalsystem angehörige
Zifferstellen zu berechnen, wie solche, die in Grade oder Stunden eingetheilt sind;
und sie druckt dann ebenfalls die Stunden oder Grade, Minuten und Secunden, letztere
bis auf eine Decimalstelle. Wäre, z.B. die Zahl 172345598714087 auf der obersten
Horizontalreihe angezeigt, so würde im betreffenden Fall stereotypirt werden
172°34'55'',9. Es ist erklärlich, daß sich ein solches Resultat nur durch
einen besondern, ohne
Zweifel verwickelten Mechanismus erreichen läßt, da die Zehnerstelle der Secunden
und Minuten nicht weiter wie 6 gehen darf, wo dann eine Einerübertragung zur Linken
erforderlich ist. Und sobald bei den Graden die Zahl 360 voll geworden ist, müssen
die Ziffern 3 und 6 wieder aus der Tafel verschwinden oder zu 0 werden. – Es
läßt sich in der That die Fülle von Scharfsinn und Ausdauer, welche alle diese
Schwierigkeiten zu überwinden gewußt, nicht hoch genug schätzen und bewundern!
Eine der vielen merkwürdigen Eigenschaften, in deren Besitz man die Maschine
nachträglich gefunden hat, ist, daß sie Zahlengleichungen lösen kann, welche
rationelle Wurzeln besitzen. Um eine derartige Rechnung auszuführen, gibt man der
Unbekannten x nach einander die Werthe 1, 2, 3 etc. und
berechnet aus dem Zahlenwerth der Function, welchen man so erhält, eine hinreichende
Anzahl von Differenzen, die man alsdann in die Maschine einsetzt. Bringt man die
Maschine nun in Gang, so wird die Tafel die aufeinanderfolgenden Werthe der
Gleichung für die fortschreitenden ganzen Zahlen der Unbekannten x aufweisen und am Ende auch einen oder mehrere Werthe
geben, die mit dem durch die ursprüngliche Gleichung gegebenen Werth der Function
zusammenfallen.
Recht interessant in dieser Hinsicht ist die von der Maschine für die Gleichung
u = x⁴ – 72 x³ + 1798 x² – 18072ˣ
ausgerechnete Tabelle, der hier der Uebersicht halber gleich
die Differenzen beigefügt worden sind.
x
u = –
1ste Differenz
2te Differenz.
3te Differenz.
4te Differ.
0
0
– 16345
3178
– 396
24
1
16345
– 13167
2782
– 372
24
2
29512
– 10385
2410
– 348
24
3
39897
– 7975
2062
– 324
24
4
47872
– 5913
1738
– 300
24
5
53785
– 4175
1438
– 276
24
6
57960
– 2737
1162
– 252
24
7
60697
– 1575
910
– 228
24
8
62272
– 665
682
– 204
24
9
62937
+ 17
478
– 180
24
10
62920
+ 495
298
– 156
24
11
62425
+ 793
142
– 132
24
12
61632
+ 935
10
– 108
24
13
60697
+ 945
– 98
– 84
24
14
59752
+ 847
– 182
– 60
24
15
58905
+ 665
– 242
– 36
24
16
58240
+ 423
– 278
– 12
24
17
57817
+ 145
– 290
+ 12
24
18
57672
– 145
– 278
+ 36
24
x
u = –
1ste Differenz
2te Differenz.
3te Differenz.
4te Differ.
19
57817
– 423
– 242
+ 60
24
20
58240
– 665
– 182
+ 84
24
21
58905
– 847
– 98
+ 108
24
22
59752
– 945
+ 0
+ 132
24
23
60697
– 935
+ 142
+ 156
24
24
61632
– 793
298
+ 180
24
25
62425
– 495
478
+ 204
24
26
62920
– 17
682
+ 228
24
27
62937
+ 665
910
+ 252
24
28
62272
+ 1575
1162
+ 276
24
29
60697
+ 2737
1438
+ 300
24
30
57960
+ 4175
1738
+ 324
24
31
53785
+ 5913
2062
+ 348
24
32
47872
+ 7975
2410
+ 372
24
33
39897
+ 10385
2782
+ 396
34
29512
+ 13167
3178
35
16345
+ 16345
36
0
Diese Gleichung gibt sonach symmetrische Werthe für u von
x = + 18 an, vorwärts bis + ∞, wie rückwärts
– ∞; die Werthe von u sind zwischen x = 0 und = + 36 negativ, ist x aber negativ oder > 36, so fallen die Werthe von u positiv aus, denn für x =
– 1 und = + 37 ist u = + 19943 u.s.w. Es gibt
somit für x vier reelle positive Wurzeln, wenn u > – 57672 und < – 62937.
Für den Fall, daß u = – 57672, hat x bloß drei reelle positive Wurzeln; und wenn u > – 62937, so sind alle Wurzeln von x imaginär. Von – 57672 bis 0, als Werth von u, hat x zwei positive
Wurzeln. Ist u > 0 und positiv, so besitzt x eine positive und eine negative Wurzel.
Es ist in diesem Beispiel besonders interessant, die Beschaffenheit der Differenzen
zu untersuchen. Die vierte Differenz ist constant = 24. Die dritte ist von +
∞ bis + 18 positiv und von da – ∞ wird sie negativ. Die zweite
Differenz ist nur in der Mitte, wo die Tabelle symmetrisch verläuft, einige Glieder
hindurch negativ, sonst bis + und – ∞ aber positiv. Endlich besitzt
die erste Differenz nach den Extremen hin entgegengesetztes Zeichen, welches aber
nochmals nach der Mitte zu sich symmetrisch umkehrt. – Es muß jedoch noch
bemerkt werden, daß, da die Werthe von u, welche die
Maschine für x = 0 bis x =
36 berechnete, negative sind, sie aber nicht als Complemente, sondern in ihrer
wahren Form berechnet und gedruckt wurden, deßhalb die Differenzen mit umgekehrten
Zeichen, also die zweite und vierte negativ oder in ihren Complementen, die erste
und dritte aber mit positivem Zeichen in die Maschine hatten eingesetzt werden müssen. Wäre
die Maschine noch weiter, wie bis zum 36sten Glied bewegt worden, so hätte man
jetzt, um positive Werthe von u zu erhalten, wieder
umgekehrt verfahren, d.h. für die vier Differenzen ihre in der Tabelle angegebenen
wirklichen Zahlenwerthe setzen müssen.
In dem so eben citirten Beispiel ist die vierte Differenz constant, und läßt sich in
die Maschine vollständig einsetzen. Es kann aber der Fall eintreten, daß man mit
Differenzen von mehr als fünfzehn Stellen zu rechnen hat, obwohl vielleicht bloß
vier, fünf, sechs, sieben oder höchstens acht Ziffern als Tafelwerth für u zu drucken sind.
Wenn die Maschine in solch einem Fall eine lange Zeit hindurch im Gange erhalten
wird, so daß sie sehr viele Werthe von u berechnet, so
wird augenscheinlich die Auslassung der 16ten etc. Zifferstelle sich bald in der
Zahlentafel fühlbar machen müssen.
Um dem vorzubeugen, muß man zu erfahren suchen, wie viele Werthe von u ohne Fehler in der letzten Ziffer des gedruckten
Resultats erhalten werden können.
Denkt man sich zu dem Zweck die Maschine in Gang gesetzt mit nur einer Differenz D der vierten Ordnung, wie es die erste Verticalspalte
andeutet,
1
2
3
4
5
ntes Glied
0
0
1 D
5 D
15 D
(n – 2)/1 . (n – 1)/2 . n/3 . (n + 1)/4 . D
0
0
1 D
4 D
10 D
(n – 2)/1 . (n – 1)/2 . n/3 . D
0
1 D
3 D
6 D
10 D
(n – 1)/1 . n/2 . D
0
1 D
2 D
3 D
4 D
(n – 1)/1 . D
D
D
D
D
D
D
so würde man, in der Art wie die Maschine die Differenzen
verbindet (in gleichzeitig gebildeten Paaren), die zweite, dritte, vierte, fünfte
und nte Colonne erhalten, wo die Coefficienten von D nothwendig und augenscheinlich figurirte Zahlen der
verschiedenen Ordnungen sind (hier bis zur fünften), nur daß die vierten und fünften
figurirten Zahlen den zweiten und dritten ein Glied vorausgesetzt sind (siehe S. 255).
Das Gesetz für irgend eine Maschine die irgend eine Ordnung von Differenzen hat,
wird daraus klar. Man sieht nun unmittelbar, daß, im Falle in die Maschine die
Differenzen D⁰, DI, DII, DIII, DIV eingesetzt wurden, die nte gedruckte Zahl, welche mit Pn, bezeichnet
worden, in Pn = D⁰ +
(n – 1)/1 DI + (n – 1)/1 .
n/2 DII + (n – 2)/1
. (n – 1)/1 . n/3 .
DIII + (n – 2)/1 . (n
– 1)/2 . n/3 . (n +
1)/4 DIV erhalten
wird. Daraus ergibt sich denn, daß wenn der Fehler wegen Auslassung der sechzehnten
etc. Ziffer in der ersten Differenz = α ist und
β, γ, δ beziehungsweise in der zweiten, dritten und
vierten Differenz, der Fehler in Pn, bezeichnet mit e, immer kleiner wie nα +
n²/2 β + n³/6 γ + n⁴/24 δ seyn sollte.
Da man die Maschine nun immer bis u ± 1/2 e statt u im Gang erhalten
kann, indem man in solcher Weise die Wirkung eines Fehlers halbirt, so kann man,
selbst wenn man mit allen vier Differenzen arbeitet, für den praktischen Gebrauch
ganz wohl e = n⁴/48
δ setzen (d.h. halb so groß wie den durch die
vierte Differenz verursachten Fehler; streng genommen wäre
Textabbildung Bd. 156, S. 326
Ist nun m die in der Tafel erforderliche Zifferzahl, so
ist es gebräuchlich, keinen größeren Fehler wie ± 5 in der m + 1ten Stelle zu erlauben. Der größte Werth, welchen
δ in der Maschine von Scheutz haben kann, ist (weniger als) 5 × 10–¹⁶, woraus man schnell
sieht, daß, da alsdann 5 × 10–m-
¹ = n⁴/48 . 5 × 10–16 ist, u⁴ = 48 × 10¹⁵–m
seyn wird. Will man somit z.B. acht Zifferstellen die Maschine correct drucken
lassen, so hat man n⁴ = 48 × 10⁷ =
480000000 und n = 148 als die Anzahl von Werthen von u, die man in jeder Richtung drucken kann.
Sollen bloß sieben Stellen correct ausfallen, so wird n⁴ = 48 × 10⁸ und n =
263.
Wünscht man bloß fünf Stellen richtig zu erhalten, so wird n = 832, so daß man in diesem Fall wenigstens 800 Glieder bei jedem
Vorwärts- und Rückwärtsschreiten der Maschine erhalten kann, oder im Ganzen
1600 Glieder. Im
Folgenden soll nun eine ganz allgemeine und in der Anwendung äußerst einfache
Methode mitgetheilt werden, wie man geeignete Differenzen finden kann, mit denen man
die Maschine in Gang setzt.
Es sey u₀ der bekannte Werth für irgend ein Glied
der Tabelle und u
x der ebenfalls bekannte Werth für ein
anderes, welches x Glieder in auf- oder
absteigender Folge entfernt ist, so läßt sich bekanntlich setzen ux = u₀ + ax + bx² + cx³ +
dx⁴.
Gibt man nun in dieser Gleichung x nach einander die
Werthe 0, ± 1 und ± 2, ordnet tabellarisch und stellt die Differenzen
der einzelnen Glieder neben einander, so erhält man folgendes Schema:
1ste Differenz.
2te Differenz.
3te Differ.
4te Diffr.
u–2 =
u₀ – 2a + 4b – 8c + 16d
a – 3b + 7c –
15d
u–1 =
u₀ – a + b
– c + d
2b – 6c + 14d
a –
b + c
– d
6c – 12d
u₀ = u₀
––––––––––––––
2b +
14d
–––––––––
24d
a + b + c + d
––––––––––––
6c + 12d
–––––––
u₁ = u₀ + a + b + c
+ d
1b + 6c + 14d
a + 3b + 7c + 15d
u₂ = u₀ + 2a +
4b + 8c + 16d
Wollen wir nun aus diesen Differenzen die Werthe der Coefficienten a, b, c und d finden, so
müssen wir berücksichtigen, daß es nicht alle ersten Glieder sind, welche in die
Maschine eingesetzt werden, sondern daß die erste und zweite Differenz der dritten
und vierten um ein Glied voraus sind. Bezeichnet man die in die Maschine
einzusetzenden und in obigem Schema unterstrichenen Glieder beziehungsweise mit DIVu–2, DIIIu–2, DIIu–2, DIu–2, von Rechts
nach Links, so ergibt sich schnell d = 1/24 DIVu–2; c = 1/6 DIIIu–2 + 2d; b = 1/2
DIIu–, – d und
a = DIu–1 + 1/2 DIIu–1 – c.
Wenn nun ferner N – 1 die Anzahl der zwischen u₀ und u ± 1,
u + 1 und u ± 2
einzuschaltenden Glieder ist, so setzt man 1/ N = x und bekommt unmittelbar:
D
IV
u
–2
x
= 24 dx⁴,
D
III
u
–2
x
= 6 (cx³ – 2dx⁴),
DIIu–x
= 2 (bx² + dx⁴),
DIu–x
= ax – bx + cx³ – dx⁴
Mit diesen Differenzen kann man nun die Maschine in Gang setzen und vorwärts von u₀ über u₁ bis
u₂ drucken und nachdem die Zeichen der
ungeraden Differenzen, wie früher gezeigt, gewechselt sind, ebenso rückwärts von u₀ über u–1 bis u–2 und zwar ohne nur die Form der Function zu
kennen, die berechnet wird, da es vollkommen hinreicht, daß man fünf bekannte Werthe
derselben in gleichen Zwischenräumen nimmt.
Ein Beispiel wird den Gebrauch obiger Formeln erläutern.
Es sollen die siebenstelligen Logarithmen von der Zahl 3000 an berechnet werden.
Man nehme N = 200 (also x =
1/200) und erhält demnach aus den anderweitig bekannten Logarithmen das folgende
Schema:
1ste Differenz.
2te Differenz.
3te Differenz
4te Differenz.
log. 2600 = 3,4149733
0,0321847
log. 2800 = 3,4471580
– 0,0022214
0,0299633
+ 0,0002868
log. 3000 = 3,4771213
– 0,0019346
– 0,0000520
0,0280287
+ 0,0002348
log. 3200 = 3,5051500
– 0,0016998
0,0263289
log. 3400 = 3,5314789
Es ist somit:
DIu–1
= 0,0299633;
DIIu–1
= – 0,0019346;
DIIIu–2 =
0,0002868;
DIVu–2 =
– 0,0000520.
Die Berechnung der Formeln würde schematisch folgendermaßen vorzunehmen seyn:
DIu–1 + 1/2
DIIu–1
– c = a
ax – bx² + cx³ – dx⁴ = DIu–x
DIIu–1 . 1/2
– d = b
bx² . 2 + 2dx⁴ = DIIu–x
1ste Differenz
2te Differenz
x = 1/200
x² = 1/4 .
(1/100)²
D
I
u
–1
= + 0,0299633..
D
II
u
–1
= – 0,0019346
1/2 DIIu–1
= – 0,0009673..
1/2 DIIu–1
= – 0,0009673
––––––––––––
d
= – 0,000002166..
+ 0,0289960..
––––––––––––––
c
= + 0,000043466..
b
= – 0,000965133..
––––––––––––––
bx²
= – 0,00..24128333;3
a
= + 0,28952533
2bx²
= – 0,00..48256666;6
ax
= +
0,000144762666666
2dx²
= – 0,00
. . . 002;7
bx²
= – 0,000000024128333
––––––––––––––––
cx³
= + 0,000000000005433
–DIIu–x
= – 0,00..48256669;3
dx⁴
= +
0,0 . . . . . 0001
Complement:
––––––––––––––––––
– DIIu–x
= + 9,99..91743330;7
D
I
u
–x
= + 0,000144786800434
––––––––––––––––––
––––––––––––––––––––
– DIu–x
= – 0,000144738543765
Complement:
– DIu–x
= + 9,999855261456235
––––––––––––––––––––
(DIIIu–2 + 1/2 DIVu–2) 1/6 = c(c . x³ – 2dx⁴) .
6
= DIIIu–2x
DIVu–2 .
1/24 = d
d . x⁴ .
24 = DIVu–2x
3te Differenz
4te Differenz
x³= 1/8 .
(1/100)³
x⁴ = 1/16
. (1/100)⁴
D
III
u
–2
= + 0,0002868
D
IV
u
–2
= – 0,0000520..
1/2 DIVu–2
= – 0,0000260
d
= – 0,0000021667..
––––––––––––
dx⁴
= – 0,00 . . . 1;354
+ 0,0002608
– DIVu–2x
= – 0,00 . . 32;496
c
= + 0,0000434666...
cx³
= + 0,0000..5433;33..
Complement:
2du⁴
= – 0,0000. . . .
2;71
– DIVu–2x
= + 9,99 . . 967;504
–––––––––––––––
–––––––––––––––––
+ 0,00 ... 5436;04
D
III
u
–2x
= + 0,00 ..32616;24
–––––––––––––––––
– DIIIu–2x
= – 0,00 ..32583;
Complement:
– DIIIu–2x
= + 9,99..967417;
–––––––––––––––––
Die Rechnung für die erste Differenz ist fünf Decimalstellen weiter ausgedehnt als
nöthig ist, um zu zeigen wie cx³ und dx⁴ erforderlichenfalls eintreten würden;
und aus einem ähnlichen Grunde sind die Rechnungen für die zweite und dritte
Differenz beziehungsweise vier und drei Stellen weiter ausgedehnt. Das Semikolon
deutet hier die fünfzehnte oder letzte Zifferstelle der Maschine an.
Werden die Logarithmen von 3000 an in aufsteigender Reihenfolge berechnet, so hat man
die Differenzen
D
I
=
,000144786800434
D
II
=
,999999951743330
D
III
=
,000000000032616
D
IV
=
,999999999999967
in die Maschine einzusetzen. Da die 4te und 2te Differenz
negativ sind, so müssen ihre Complemente genommen werden. Rechnet man aber in
absteigender Folge, also von 3000 gegen 2800 etc. hin, so muß man berücksichtigen, daß in diesem
Falle die dritten und ersten Differenzen ebenfalls negativ werden, also mit den
vierten und zweiten gleiches Zeichen erhalten. DIu–x, sowie DIIIu–2x bekommen
deßhalb einen von dem früheren etwas verschiedenen Werth. In die Maschine müssen
jetzt für alle vier Differenzen ihre entsprechende Complemente eingesetzt
werden.
D
I
=
,999855261456235
D
II
=
,999999951743330
D
III
=
,999999999967417
D
IV
=
,999999999999967.
Die Maschine rechnet auf diese Weise ohne Fehler die Logarithmen von 2600 bis 3400,
im Ganzen 800 Glieder.
In ähnlicher Weise sind die von Gravatt herausgegebenen
fünfstelligen Logarithmen von 1 bis 10000 berechnet und gedruckt worden. Die ganze
Zeit, welche diese gleichzeitige Operation in Anspruch nahm, betrug beinahe achtzig
Stunden.
Für den Gebrauch der Maschine ist noch folgender Punkt zu erörtern. Es kann
eintreten, daß u, die Funktion von x, welche zu berechnen ist, nicht die vierte, noch
überhaupt irgend eine Ordnung von Differenzen constant hat. Um die Folgen davon
einzusehen, sollen, wie es in den meisten Fällen völlig ausreichend seyn wird, die
Werthe von ux,
abgeleitet von vier Ordnungen von Differenzen (hier gezeichnet IVux) mit den Werthen von ux, abgeleitet von sechs
Ordnungen von Differenzen (gezeichnet VIux) verglichen
werden.
Setzt man in der Gleichung
ux =
u₀ + ax¹ +
bx² + cx³
+ dx⁴ + ex⁵ +
fx⁶
in ähnlicher Weise wie früher x
nach einander 0, ± 1, ± 2 und ± 3, so findet man in den
einzelnen Differenzen seine Coefficienten:
f = 1/720
DVIu–3
e = 1/120
DVu–3 + 1/240
DVIu–3
d = 1/24
DIVu–2 – 1/144
DVIu–3
c = 1/6 DIIIu–2
+ 1/12
DIVu–2 + 1/24
DIVu–3 – 1/18
DVIu–3
b = 1/2
DIIu–1 – 1/24
DIVu + 1/180
DVIu–3
a = DIu–1 + 1/2
DIIu–1 – 1/6
DIIIu–2 – 1/12
DIVu–2 + 1/30
DVu–3 + 1/60
DVIu–3
Setzt man nun
u₀ + ax + bx² + cx³ + dx⁴ + ex⁵ + fx⁶ =
u₀ + αx +
βx² + γx³ + δx⁴
was streng genommen nur richtig ist für x = 0, ± 1 und ± 2, aber bis zu einem gewissen Grad der
Annäherung auch für andere Werthe von x, so erhält man,
da nach dem vorhergehenden
δ = 1/24
DIVu–2,
γ = 1/6
DIIIu–2;
β = 1/2
DIIu – 1/24
DIVu
α = DIu–1 + 1/2
DIIu–2 – 1/6
DIIIu–2 – 1/12
DIVu–2
direct den Unterschied der beiden Functionen:
VIu–x – IVu–x
= 1/720
DVIu–3x6 + (1/120
DVu–3 + 1/240
DVIu–3) x5
–
– 1/144
DVIu–3x4 + (1/24
DVu–3 + 1/148
DVIu–3) x3 +
+ 1/180
DVIu–3x2 + (1/30
DVu–3 + 1/60
DVIu–3) x =
= 1/720
DVIu–3
{x6
+ 3x5 –
5x4
– 15x3
+ 4x2 + 12x} +
= 1/120
DVu–3
{x5 – 5x3 + 4x}
Man sieht nun leicht ein, daß die Fehler, die durch den Gebrauch von vier Differenzen
entstehen, wo man sechs hätte anwenden müssen, nahezu Maxima seyn werden in der Mitte zwischen den Werthen von x = 0 und ± 1, von + 1 und + 2, sowie von
– 1 und – 2. Setzt man somit in obige Formel nach einander x ± 1/2 und ± 3/2, so findet man
genau:
VIu1/2 – IVu1/2 = 3/256
DVu–3 + 7/1024
DVIu–3
VIu–1/2 – IVu–1/2 = – 3/256
DVu–3 + 5/1024
DVIu–3
VIu3/2 – IVu3/2 =
– 7/256
DVu–3 – 21/1024
DVIu–3
VIu–3/2 – IVu–3/2 = 7/256
DVu–3 + 7/1024
DVIu–3
oder für die praktische Anwendung kann man den halben Fehler setzen
0,001 ( 6 DVu–3 + 3
½ DVIu–3)
zwischen u0
und u1
0,001 (– 6 DVu–3
– 2 ½ DVIu–3)
zwischen u0
und u–1
0,001 (– 14 DVu–3
– 10 ½ DVIu–3)
zwischen u1
und u2
0,001 ( 14 DVu–3 + 3
½ DVIu–3)
zwischen u–1 und u–2
Diese Fehler müssen natürlich aus den Tafeln weggelassen werden; d.h. man wird eine
Zifferstelle weniger anwenden, als die mit dem Fehler behaftete.
––––––––––
Wir hatten unsern Bericht schon so weit beendet, als uns von Hrn. Donkin, den wir brieflich um einige Details über die von
ihm für das Register Office construirte Maschine ersucht
hatten, eine Beschreibung derselben zugeschickt wurde, die erst kürzlich, am 22.
März, in den Dealy News erschienen war. Da jedoch keine
erläuternden Zeichnungen beigefügt sind, so bleibt immerhin das Ineinandergreifen
der Maschinentheile unverständlich und wir vermögen darnach nur die den früher
citirten Specimens of Tables entnommene perspectivische
Zeichnung, Fig.
1 auf Tab. V, einigermaßen zu erläutern. Die ganze Maschine ist etwa sechs
Fuß lang, zwei Fuß hoch und zwei Fuß tief, ihr Gewicht gegen 8 Centner. Der
rechnende Theil besteht aus fünf Reihen versilberter Ringe oder hohler Cylinder,
jeder etwa zwei Zoll im Durchmesser und drei viertel Zoll hoch, worauf die 10
Zifferzeichen eingravirt sind. In jeder Horizontalreihe befinden sich fünfzehn
Zifferringe. Dieselben ruhen auf einer Messingbank und bewegen sich zugleich auf
derselben im Kreise. Eine einzige Stahlachse geht durch je fünf senkrecht
übereinander stehende Zifferringe und durch die Messingbänke, auf denen sie ruhen,
hindurch und bewirkt die Bewegung der Ringe. Die Ziffern auf jedem der 15 Ringe der
ersten, dritten und fünften Reihe sind in umgekehrter Folge, 1, 2, 3 etc. von Rechts
nach Links markirt; die Ziffern auf der zweiten und vierten Reihe hingegen in
natürlicher Reihenfolge von Links nach Rechts. Wenn nun die Maschine durch Umdrehung
der Kurbel in Gang gesetzt wird, so machen zuerst alle 15 senkrechten Stahlachsen
eine vollständige Umdrehung von Rechts nach Links und bewirken dabei, durch ein
nicht weiter erkennbares Arm- und Hebelwerk, daß sich die Zifferringe der
zweiten und vierten Reihe um eben so viele Ziffern weiter bewegen, wie die direct
darunter befindlichen Zahlen der dritten und fünften Reihe andeuten. An den Ringen,
wo eine Uebertragung von Einern stattfinden soll, ist unterdeß ein Hebel nach Hinten
vorgesprungen. Wird nun die Kurbel der Maschine weiter gedreht, so geht eine
senkrechte Pfoste mit zwei Armen vor der ganzen Zifferringreihe und eine ganz
gleiche hinter derselben in entgegengesetzter Richtung an der ganzen Länge der Reihe
einher. Die hinten stehende Pfoste gleitet mit ihren zwei Armen an den Ringen der
zweiten und vierten Reihe von Rechts nach Links schreitend hin und drückt dabei
die vorgesprungenen Hebel in ihre Ruhelage zurück, dabei zugleich die betreffenden
Zifferringe um eine Ziffer weiter bewegend. Die in der Figur sichtbare Pfoste D, deren zwei Arme an der ersten und dritten
Zifferringreihe hinstreichen, ist während dem von dem äußersten Zifferring links zu
dem äußersten rechts geschritten, ohne eine weitere Wirkung hervorzurufen. Während
der nun folgenden Kurbelumdrehung bleiben die Pfosten in Ruhe stehen, aber die 15
Stahlachsen machen wieder eine volle Umdrehung, nun jedoch in entgegengesetzter
Richtung wie vorher, also von Links nach Rechts. Dadurch ist es möglich geworden,
daß die Ringe der zweiten und vierten Reihe in Ruhe bleiben, während die der ersten
und dritten Reihe von den Achsen mitgenommen werden und zwar gerade um so viele
Zehntheile einer Umdrehung, als die Zahlen direct darunter in der zweiten und
vierten Reihe angeben. Da hierbei die Ringe der ersten und dritten Reihe ebenfalls
von Links nach Rechts sich bewegen, so folgen sich natürlich die darauf befindlichen
Zahlen in ihrer zunehmenden Folge. An den Ringen, wo ein Hinzuzählen von Einern
stattfinden soll, sind dabei wiederum kleine Hebel und zwar nach vorn vorgesprungen;
während der weiteren Kurbelumdrehung gleitet jetzt die vordere Pfoste von Rechts
nach Links mit ihren beiden Armen an der ersten und dritten Zifferringreihe einher,
drückt die vorgesprungenen Hebel zurück und bewegt dabei die betreffenden Ringe um
eine Ziffer weiter. Die hintere Pfoste gleitet zugleich von Links nach Rechts, ohne
zu wirken. Damit ist nun eine vollständige Rechnung beendet. Das Drucken der in der
obersten Reihe dargestellten Zahlen der Tabelle geschieht in folgender Weise. Die
acht ersten Ringe links sind jeder in fester Verbindung mit einem hohlen
Messingcylinder, welcher die Stahlachse frei umschließt. An seinem oberen Ende ist
eine mit besonderen Einschnitten versehene Scheibe angebracht, welche die Bewegung
der Zifferringe vermittelst zweier auf eigenthümliche Weise geformter Apparate auf
eine Zahnstange überträgt, die wiederum in ein Zahnrad B
eingreift und dieß um eben so viele Abschnitte dreht, als sich der Zifferring bewegt
hat. Mit diesem Zahnrad in unmittelbarem Zusammenhang auf horizontaler Achse bewegt
sich eine Letternwelle C, welche auf ihrer Peripherie
die zehn Ziffern in Relief als Stahlstanzen enthält. Es sind nun solcher
Letternwellen acht nahe neben einander, die durch Teleskopenachsen (wie man sie bei
den verschiedenen Zeigern einer Uhr kennt) mit ihren betreffenden Zahnrädern in
Verbindung stehen. Sowie nun die Zifferringe der obersten Reihe in Bewegung gesetzt
werden, bewegen sich gleichzeitig die acht Letternwellen, so zwar daß immer die
Zahl, welche von den Ringen angegeben ist, von den Letternwellen nach Unten gekehrt
wird. Nachdem die Rechnung vollendet ist, wird jetzt durch die Maschine ein Bret, auf
dem eine Bleiplatte liegt, in die Höhe gehoben und die berechnete Zahl in die Platte
eingestanzt. Das Bret senkt sich alsbald wieder und schreitet zugleich um einen Raum
vorwärts, welcher der Entfernung zweier auf einander folgender Zahlen
entspricht.
Es scheint aus dieser übersichtlichen Erläuterung hervorzugehen, daß die Maschine die
an sie gestellten Anforderungen auf eine sehr einfache Weise erfüllt, wie man es
kaum bei der Natur scheinbar so verwickelter Vorgänge erwarten sollte. Dem
entsprechend ist auch der Kaufpreis, welcher von Donkin
(Firma: Bryan
and
Donkin
Bermondsey, near Grangr Road, London) für die
Herstellung einer solchen Maschine verlangt wird, ein mäßiger zu nennen. Derselbe
erbietet sich nämlich, beim gleichzeitigen Zusammentreffen der Bestellung mehrerer
Maschinen, das Exemplar zu 2000 Pfund Sterling zu liefern. Die von dem englischen
Gouvernement für die an das Register Office gelieferte
Maschine bezahlte Summe von nur 1200 Pfd. St. ist eine unverhältnißmäßig niedrige
gewesen, bei der die Fabrikanten ihre Rechnung nicht finden konnten. Die Ausführung
dieser Maschine wurde wohl überhaupt nur darum unternommen, um ein Interesse dafür
in weiteren Kreisen hervorzurufen und die Möglichkeit zu beweisen, daß ein Werk,
welches einst in demselben Lande so unermeßliche Summen verschlungen hatte, ohne zur
Vollendung zu gelangen, sich auch mit mäßigen Mitteln und für ein größeres Publicum
in einer allen Anforderungen entsprechenden Weise dürfte darstellen lassen.
Hoffentlich können wir im Stande seyn, demnächst noch die näheren
Constructionsdetails dieser merkwürdigen Maschine mitzutheilen. Aus Veröffentlichung
derselben dürfte wohl kaum weder ihren Erfindern, den Herren Scheutz, noch ihrem gegenwärtigen englischen Fabrikanten ein Nachtheil
oder eine Concurrenz zu befürchten seyn; das Interesse, die Theilnahme für dieselbe
würde nur zunehmen, wenn ihr Organismus völlig verstanden ist.
Von einem Mangel muß schließlich noch diese Art von Rechenmaschine frei gesprochen
werden, von welchem alle anderen seither construirten Rechenmaschinen, die
insbesondere die Operationen der vier Species ausführen sollten, begleitet waren und
der ihrer Verbreitung ein Ziel setzte: Die Aufmerksamkeit für deren Betrieb von
Seiten des Manipulators ist nämlich zu bedeutend, zuweilen selbst anstrengend, wie
bei den Divisionsmaschinen, so daß sie häufig keine wesentliche Erleichterung und
Beschleunigung der Arbeit gewährten; und dabei litten noch die Resultate an einer
möglichen nicht zu controlirenden Ungenauigkeit, die sowohl in der Unaufmerksamkeit der Person
des Rechnenden wie in der immer aus sehr vielen beweglichen und gegen einander
verschiebbaren Theilen zusammengesetzten Maschinerie ihren Grund haben konnte. Es
fehlte damit jeder Zeit die geringste Garantie für die Richtigkeit der Rechnung, der
Vortheil, welcher in der Anwendung der Maschine liegen sollte, blieb illusorisch.
– In der Tabellen-Rechenmaschine können beide Mißstände nicht
eintreten. Die Bedienung ist eine äußerst einfache, indem, sobald von Anfang an die
Differenzen richtig eingesetzt sind, die Bewegung und Rechnung der Maschine durch
eine einfache Kurbelumdrehung stattfindet. Ferner aber sollen von der Maschine nicht
einzelne Zahlenresultate berechnet werden, sondern eine große Menge mit einander in
Verbindung stehender und sich auseinander ergebender Zahlen, von denen naturgemäß
die eine oder die andere in größeren Intervallen schon im Voraus bekannt ist, oder
auf dem gewöhnlichen Wege durch Rechnung gefunden werden kann. Indem nun die
Maschine beim Fortschreiten der Rechnung immer die eine oder die andere jener Zahlen
wieder produciren muß, und außerdem ihre Resultate zu gleicher Zeit druckt, so liegt
darin für immer eine Controle und eine Bürgschaft für die Richtigkeit ihrer Angaben
und den ungestörten Zusammenhang ihrer Theile.
Tafeln