| Titel: | Die Universal-Kuppelung von F. W. Blees. |
| Fundstelle: | Band 176, Jahrgang 1865, Nr. CXXIV., S. 419 |
| Download: | XML |
CXXIV.
Die Universal-Kuppelung von F. W. Blees.
Aus den Verhandlungen des Vereins zur Beförderung des
Gewerbfleißes in Preußen, 1865 S. 29.
Mit Abbildungen auf Tab.
VI.
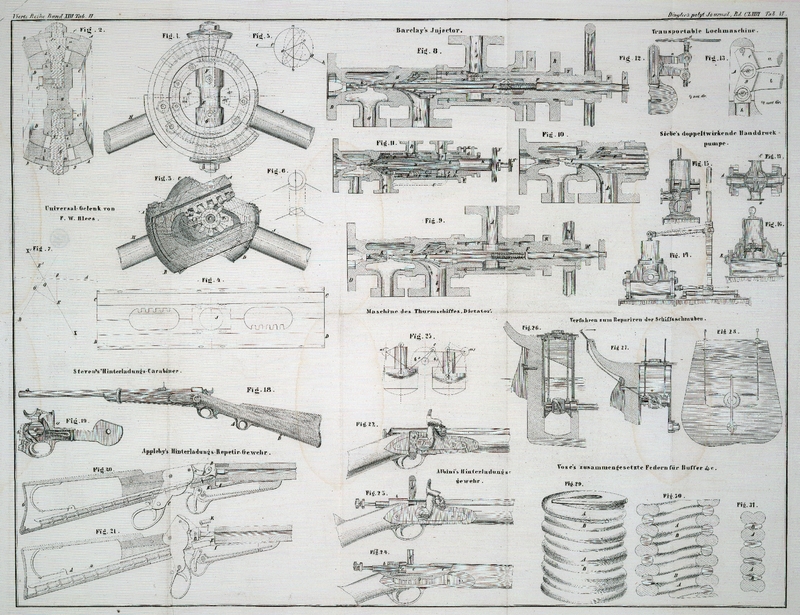
Universal-Kuppelung von F. W. Blees.
I. Beschreibung der Universal-Kuppelung;
von F. W. Blees, königl. Bergassessor und Berggeschworenen.
Der Verein zur Beförderung des Gewerbfleißes in Preußen hatte pro 1864/1865 folgende
Preisaufgabe gestellt, die Herstellung einer Universal-Kuppelung betreffend:
„Die silberne Denkmünze, oder deren Werth, und außerdem dreihundert Thaler
Demjenigen, welcher als Verbesserung des Hooke'schen
Schlüssels eine Kuppelung für Wellen, deren Drehungsachsen einander schneiden,
angibt, welche derartig eingerichtet ist, daß die Bewegung der treibenden Welle
auf die getriebene ohne Aenderung der Winkelgeschwindigkeit übertragen wird. Die
Ablenkung der getriebenen Welle von der treibenden soll während der Bewegung bis
zu einem Winkel von 45 Grad variiren können und die Construction möglichst
einfach seyn, so daß dieselbe auch für landwirthschaftliche wie andere Maschinen
von beliebiger Kraftübertragung anwendbar und praktisch ist.“
Motive: „Bei verschiedenen landwirthschaftlichen und anderartigen
Maschinen, welche durch animalische oder anderweite Kraft in Umtrieb gesetzt
werden, bedient man sich zur Uebertragung der drehenden Bewegung des sogenannten
Universal-Gelenkes oder des Hooke'schen Schlüssels.
Dieser Mechanismus, wegen seiner Einfachheit sonst wohl zu dem genannten Zwecke
geeignet, besitzt aber eine Eigenthümlichkeit, welche störend und schädlich
wirkt, diejenige nämlich, daß er bekanntlich die getriebene Welle nicht mit
gleichförmiger, sondern mit periodisch schwankender Geschwindigkeit herumführt,
der Art, daß in jedem Doppel-Quadranten ein Maximum und ein Minimum der
Geschwindigkeit eintritt, welche um so mehr von der Normal-Geschwindigkeit
abweichen, je größer der Ablenkungswinkel der beiden verbundenen Wellen ist.
Dadurch werden die getriebenen Theile in eine zuckende und rüttelnde Bewegung
versetzt, welche die Operation der getriebenen Welle in störender Weise
beeinflußt und die Maschine raschem Verschleiß aussetzt. Es wäre deßhalb
wünschenswerth, eine Kuppelung für Wellen mit sich schneidenden Drehachsen zu
besitzen, welche von diesem Nachtheile frei wäre, die mit einem Worte eine
wahrhafte Universal-Kuppelung wäre.“
Unterzeichneter, welcher eine Lösung der vorstehenden Aufgabe gefunden zu haben
glaubtDie von Hrn. Blees
eingesandte Lösung der Preisaufgabe wurde mit dem
Preise gekrönt., hält es für zweckmäßig, bei Beschreibung derselben denselben Weg zu
verfolgen, auf welchem er zu der betreffenden Idee gelangt ist.
Dieser Weg ging natürlich von einer Erörterung der Gründe der oben erwähnten
Unvollkommenheit des Hooke'schen Universalgelenkes aus,
welche man, in die Formeln der sphärischen Trigonometrie gekleidet, in Weisbach's Mechanik Bd. III S. 19
findet. Zum allgemeineren Verständniß will ich sie hier durch ein kurzes
Raisonnement entwickeln:
Textabbildung Bd. 176, S. 421
Das Hooke'sche Gelenk besteht bekanntlich aus einem
Kreuz, dessen beide Arme mittelst Scharniere an halbkreisförmige Bügel
angeschlossen sind, in welche auf den beiden entgegengesetzten Seiten des
Kreuzes die treibende und die getriebene Welle auslaufen. Denkt man sich Kreuz,
Bügel und Wellen, wie nebenskizzirt, auf mathematische Linien reducirt, so
beschreiben die Bügel, auch bei jeder Ablenkung der einen Welle von der anderen,
bei ihrer Rotation die Oberfläche einer Kugel, deren Durchmesser die Kreuzarme
und deren Mittelpunkt ihr Kreuzpunkt bildet.
Die beiden Kreuzarme beschreiben nur bei der Stellung, in welcher beide Wellenachsen
in einer Linie liegen, eine gemeinsame Kreisfläche, bei jeder Ablenkung der
Wellenachsen aber zwei verschiedene Kreisflächen, welche natürlich immer normal zu
der betreffenden Wellenachse bleiben, also einen Neigungswinkel zu einander haben,
welcher gleich dem Ablenkungswinkel der Wellenachsen ist, während ihre
Durchschnittslinie normal zu beiden Wellenachsen liegt. Hat nun, Tab. VI, Fig. 5, die
treibende Welle e, f eine gleichförmige
Umlaufsgeschwindigkeit, so bewegt sich mit Bezug auf die erwähnte Kugelfläche der
Kreuzarm a, b auch mit gleichförmiger
Bahngeschwindigkeit durch die Aequatorialebene acbd, während der an der abgelenkten getriebenen Welle g, h sitzende Kreuzarm c, d
mit Bezug auf die erwähnte Kugelfläche den größten Kreis cidk beschreibt, in welchem er während jeder
Umdrehung zweimal den Aequatorialkreis acbd
durchschneidet, zweimal aber je nach der Ablenkung der Welle das Maximum der Polhöhe
ak und bi
einnimmt und sich so mehr oder weniger dem Pole der Bewegung f nähert, wo Stillstand eintritt.
Vergleichsweise beschreiben die Endpunkte des einen Kreuzarmes a, b also mit gleichförmiger Geschwindigkeit eine Bahn, wie ein Körper,
der sich bei der täglichen Rotation der Erde im Erdäquator befindet, die Endpunkte
des anderen Kreuzarmes c, d aber mit ungleichförmiger
Geschwindigkeit, wie sie bei der gleichförmigen Erdrotation ein Körper beschreiben
würde, der sich innerhalb 24 Stunden mit gleichförmiger Geschwindigkeit von einem
Orte mit beliebiger Polhöhe der südlichen Hemisphäre auf einem Meridiane bis zur
gleichen Polhöhe der nördlichen Hemisphäre und ebenso wieder zurück bewegte. Ein
solcher Körper würde einen den Aequator schneidenden größten Kreis beschreiben, in
welchem zwei Maxima der Geschwindigkeit eben in diesen Durchschnittspunkten, zwei
Minima der Geschwindigkeit aber bei Erreichung der größten Polhöhe, wo die Meridiane mehr
zusammenrücken und die Rotationskreise kleiner werden, stattfänden.
Diese Erörterung führte mich auf die Bemühung, bei dem neu zu construirenden Gelenke
die Mittheilung der Bewegung also nicht, wie hier, durch ein Kreuz stattfinden zu
lassen, dessen Arme einzeln eine constante Lage zu den beiden Wellen haben, sondern
durch einen Apparat, der in seiner Stellung variabel und so angeordnet sey, daß
seine Stellung zu den beiden Wellen immer eine vollkommen symmetrische bliebe. Ich
dachte mir also die Bügel der beiden Wellen, wie in Fig. 6 skizzirt, in eine
Ebene gelegt und zu Ringen ergänzt und durch einen Bolzen zur Uebertragung der
Bewegung verbunden, der zu beiden Wellen symmetrisch läge. Es kam also darauf an,
die Construction so zu machen, daß die Rotation der Wellen unbehindert stattfinden
könne und daß der Bolzen zur Uebertragung der Bewegung immer in der symmetrischen
Lage erhalten werde, zu welchem Behufe er bei der Rotation also immer in derjenigen
Ebene bleiben muß, welche den von den beiden Wellenachsen gebildeten auch variablen
Winkel halbirt. Der eine Ring mußte offenbar größer werden als der andere um ihn zu
umfassen, da die Ringebenen bei jeder Stellung während der Rotation sich
durchschneiden, mit Ausnahme von nur zwei Durchgangsmomenten während jeder
Umwälzung, welche jedesmal nach Umdrehung um 180° eintreten und in welchem
sie in eine Ebene fallen. Die Achse des die Bewegung übertragenden Bolzens muß
offenbar immer mit der Durchschnittslinie der beiden Ringebenen zusammenfallen. Auch
mußte der größere Ring auf- und ausgeschnitten werden, um die Rotation bei der
Ablenkung der Wellen bis zu 45° von einander zu erlauben. Der Anblick der
Skizze lehrte schon, daß der Bolzen bei dieser Stellung Ringstücke von ungleicher
Länge auf beiden Seiten jeder Welle abschnitt. Er mußte also während der Rotation
auf den Ringen sich verschieben, oscilliren können. Ferner verlangte die Bedingung,
ihn stets in der Halbirungsebene des Wellenachsen-Winkels zu erhalten, daß er, um
obiges Bild festzuhalten, stets gleiche Polhöhe auf den beiden rotirenden Ringen, beziehungsweise auf den beiden durch die rotirenden Ringe beschriebenen Kugelflächen behalte,
welche einen gemeinsamen Mittelpunkt, aber verschiedene Drehungsachsen haben.
Dieß Alles wurde durch die Idee erreicht, Ringe und Bolzen mit einer Verzahnung zu
versehen, und alle übrige Construction ergab sich nun von selbst so, wie ich es auf
dem beigegebenen Risse dargestellt habe.
Dieser Riß, Tab. VI, stellt die Kuppelung so dar, wie sie wohl aus Schmiedeeisen
hergestellt werden möchte, wahrend das von mir dem Verein für Gewerbfleiß eingesandte Modell sie so gibt,
wie sie wohl in Guß (Eisen- oder Gelbguß) auszuführen seyn dürfte.
Figur 1 gibt
einen Grundriß der Kuppelung, beide Ringe in einer Ebene liegend und die
Wellenachsen in einer äußersten Ablenkung, die eine nämlich um 45° von der
Verlängerung der anderen abgelenkt.
Figur 2 gibt
einen Durchschnitt durch die Achse des Treibbolzens.
Figur 3 gibt
einen Grundriß nach erfolgter Drehung der Ringe um 90°, welcher den
Mechanismus eher zu veranschaulichen geeignet ist, als es ein der Fig. 1 entsprechender
Aufriß seyn würde, bei welchem die Ringe in einer Ebene liegen würden.
Fig. 4 gibt
eine aufgerollte innere Ansicht des inneren Ringes zur Veranschaulichung der
Zahnanordnung etc.
Da alle Linien der Verzahnung nach dem Durchschnittspunkte der Achsen der beiden
rotirenden Wellen, welcher zugleich der gemeinsame Mittelpunkt der durch die beiden
Ringe zu, beschreibenden Kugelflächen ist, convergiren müssen, so mußte sie also
eine conische werden.
Der Treibbolzen besteht, besonders bei seiner Herstellung in Guß, aus drei, übrigens
durch die Schrauben e₁ und e₂ zu einem in sich unbeweglichen Ganzen verbundenen Theilen, den
beiden conischen Getrieben oder Ritzeln f₁ und
g₁ welche mit ihrem verlängerten Kern F und G in das Mittelstück
E eingesetzt sind. Da der Bolzen eine zweifache
Bewegung erhält, nämlich eine um seine Achse recht- und rückläufig rotirende und
eine mit Bezug auf die Ringebenen um seinen Mittelpunkt oscillirende, so müssen
seine Enden auch, und ebenso die Innenseite des inneren Ringes, so weit sie von ihm
bestrichen wird, nach den Kugelflächen f, g, h und i (Fig. 2) gekrümmt seyn.
Alle Kugelflächen des Apparates erhalten natürlich einen allen gemeinsamen
Mittelpunkt.
Die Ringe bestehen, um die Verzahnungen und die Ring-Schlitze, in welchen der Bolzen
hin und her schwingt, herstellen zu können, aus einer oberen und einer unteren
Hälfte, der äußere aus A und B, der innere aus C und D. Ich habe die Ringe, um eine gleichmäßigere Stärke zu erzielen, der
Convergenz der conischen Ritzel entsprechend oben und unten nach innen conisch
abgeschrägt. Dieß erschwert etwas die Construction, ist aber auch unwesentlich, und
sie können eben so wohl oben und unten nach einer ebenen Fläche geformt werden.
Wenn die Ringe sich genau umschließen, was allerdings für die Solidität der
Construction wünschenswerth seyn dürfte, so muß die Außenseite des inneren und die
Innenseite des äußeren Ringes ebenfalls nach einer Kugelfläche geformt und abgedreht
werden. Es läßt sich nicht läugnen, daß dieß die Construction einigermaßen
complicirt macht. Wenn
man dieß aber absolut vermeiden will, kann es auch geschehen; man braucht dann nur
einen so weiten Zwischenraum zwischen beiden Ringen zu lassen (wobei die conischen
Ritzel natürlich um ein Gleiches verlängert werden müssen), daß sie nach
Cylinderflächen geformt sich bei ihren Drehungen und Durchkreuzungen nicht berühren
und hindern. Dasselbe gilt von der Innenseite des inneren und der Außenseite des
äußeren Ringes.
Die Höhe der Schlitze der Ringe, in welchen der Bolzen hin- und hergehen soll,
entspricht dem Durchmesser der conischen Ritzel, ist innen also auch kleiner als
außen. Die Länge dieser Schlitze muß gleich werden der äußersten Ablenkung der einen
Welle, d.h. einem Bogen von 45° plus dem
Durchmesser des conischen Getriebes.
Die Anordnung der Verzahnung dieser Schlitze, welche sich, beiläufig bemerkt, genau
decken, wenn die Wellenachsen in einer Linie liegen, ist eine derartige, daß der
eine Schlitz jedes Ringes unten, der andere oben gezahnt ist, und daß auf der Seite,
wo der innere Ring unten gezahnt ist, der äußere Ring oben seine Zähne hat und
umgekehrt, wie die Zähne aa, bb, cc, dd, Fig. 2, 3 und 4 dieses andeuten.
Hierdurch ist es möglich gemacht, daß die conischen Ritzel nicht in einander
entgegengesetztem Sinne sich zu drehen und beweglich zu seyn brauchen, sondern mit
dem Mittelstück E zu einem Ganzen verbunden seyn können,
so daß sie sich immer im gleichen Sinne drehen.
Ueber die kugelflächigen Enden dieses Mittelstückes E
greift (Fig.
2) der innere Ring über, während in den äußern Ring die mit Schraubenmuttern
befestigten die conischen Ritzel bedeckenden Leitscheiben ff, dd (Fig. 1 und 2, in Fig. 3
fortgenommen) eingelassen sind. Diese Leitscheiben sind auf ihrer Innen- und
Außenseite nach Kugelflächen, am Rande nach einer Kugelfläche geformt und haben ein
Loch in der Mitte zum Durchlassen des Schraubenansatzes der Ritzel. Diese
Einrichtungen bewirken eine vollkommene Leitung der conischen Ritzel in den
Schlitzen des inneren und äußeren Ringes, so daß der richtige Abstand und Spielraum
in den Verzahnungen gewahrt bleibt. Werden die entsprechenden nuthenförmigen
Vertiefungen an der Innenseite des inneren und an der Außenseite des äußeren Ringes
auf der Drehbank hergestellt, so werden sie natürlich rund herum gehen. Da dieses
auch die Construction erschwert, kann man den Zweck auch durch angegossene oder
anzuschraubende Leisten über und unter den Aufschlitzungen der Ringe bewirken.
Die Aufeinanderbefestigung beider Hälften jedes Ringes kann, wie in der Zeichnung
angedeutet ist, durch bogenförmig gekrümmte Schraubenbolzen geschehen, für welche in
jede Ringhälfte die Löcher von oben und unten in gebrochener Linie eingebohrt werden können.
Werden die Ringe gegossen; so können sie auch besondere Ansätze zur Aufnahme gerader
Schraubenbolzen erhalten.
Die Befestigung der Wellen H und I an den Ringen kann, wie im Risse angedeutet (Fig. 1, 2 und 4), durch einen zwischen
die Ringhälften einzuschaltenden und festzuschraubenden keil- und krückenförmigen
Ansatz der ersteren oder auch, wie an dem von mir eingesandten Modelle, mit einer
Muffenverbindung mit durchgestecktem Keil geschehen. Die Construction muß aber immer
so gewählt werden, daß die Welle am inneren Ringe einen nicht zu großen Durchmesser
erhält, weil sonst der äußere Ring noch mehr ausgeschnitten werden müßte. Der
Ausschnitt muß nämlich den doppelten Ablenkungswinkel von 45° plus dem Wellendurchmesser, d. i. 90 + circa 30° = circa
120°, betragen. Derselbe muß bei dem Erforderniß der Möglichkeit einer
Ablenkung von 45°, wie man aus der Zeichnung ersieht, schon so bedeutend
seyn, daß die Schlitze des äußeren Ringes an der einen Seite offen seyn müssen, weil
kein Platz bleibt für eine Verstärkung zu ihrem Verschlusse. Dieses, was im
Interesse einer starken Construction zu wünschen wäre, wird aber wohl möglich, wenn
man sich mit dem erforderlichen Ablenkungswinkel von circa 30° zufrieden gibt, wobei der jetzt gabelförmig offene
Schlitz des äußeren Ringes durch einen Ansatz beider Ringhälften mit durchgestecktem
Schraubenbolzen ebenfalls geschlossen werden könnte.
Man sieht aus Vorstehendem, daß das Princip dieses Mechanismus zwar ein äußerst
einfaches ist, so einfach, daß es schwer fällt, an seine Neuheit zu glauben, daß
aber die Ausführung desselben eine schon etwas complicirte Construction erheischt,
welche namentlich durch die Kugelflächen und conischen Verzahnungen bedingt ist.
Auch werden die Verzahnungen mit der Zeit durch Abnützung Roth leiden. Ich habe den
beabsichtigten Zweck, den Bolzen in seiner richtigen Bewegungsebene zu halten, durch
keinen anderen einfacheren Mechanismus zu erreichen gewußt, als durch diese
Verzahnung. Es hätte freilich auch wohl durch Lenkstangen von beiden Wellen aus
bewirkt werden können, jedoch nur mit noch größerer Complicirtheit.
Man wird aber billigerweise zugeben müssen, daß die vier Gelenke oder Scharniere des
Hooke'schen Gelenkes, welche bei Ausführung in
größerem Maaßstabe auch mit Achsfuttern versehen werden müssen, auch der Abnützung
unterworfen sind und diesen Apparat auch nicht gerade als einen sehr einfachen
erscheinen lassen.
Es wird sich fragen, ob der vorgesteckte Zweck sich auf noch einfachere Weise wird
erreichen lassen und ob die größere Complicirtheit des oben beschriebenen neuen
Mechanismus durch den Vortheil der erzielten gleichförmigen Wellenbewegung als
ausgeglichen zu betrachten ist.
Als wissenschaftlich nicht ohne Interesse hebe ich noch hervor, daß der Treibbolzen,
welcher die gleichförmige Bewegung der einen Welle gleichförmig auf die andere
überträgt, – eine Gleichförmigkeit, welche sich nur auf die bei beiden
Wellenachsen verschiedenen und auf diese senkrechten Rotationsebenen bezieht, daß
dieser Bolzen selbst, sage ich, eine ungleichförmige Bewegung, wie der zweite Arm
des Hooke'schen Gelenkkreuzes mit zwei Maximis und zwei
Minimis der Geschwindigkeit hat, da er seine Bewegung zwar von der gleichförmig
bewegten Welle erhält, sich aber nicht in deren Rotationsebene, sondern in einer
diese durchschneidenden ebenen Fläche bewegt. Die erzielte Gleichförmigkeit wird,
wie schon oben gesagt, nur dadurch bedingt, daß letztere Ebene den Winkel der
Wellenachsen und der besagten Rotationsebenen halbirt und daß die Bolzenachse mithin
zu beiden Wellen- und Rotationsachsen immer gleiche Polhöhe hält und also immer
vollkommen symmetrisch zu denselben liegt.
Außer diesem Raisonnement, welches die Sache wohl hinreichend klar machen dürfte,
auch noch den Beweis für die Richtigkeit der Lösung der gestellten Aufgabe in
mathematische Formeln gekleidet zu geben, erlaube ich mir für überflüssig zu
halten.
Schließlich bemerke ich noch, daß sich meines Erachtens der Fehler des Hooke'schen Gelenkes übrigens dadurch vollkommen
paralysiren läßt, daß man dasselbe repetirt, d.h. ein doppeltes Gelenk daraus
macht.Eine bekannte Einrichtung, siehe u.a. Willis' princ. of mechanism. London
1841.Anm. d. Red. der Verhandlungen des Vereins. Freilich müssen dann die Bügel des Mittelstückes in eine Ebene zu liegen
kommen, so daß die Bügel der beiden Wellen immer eine vollkommen symmetrische Lage
zu einander haben. Wollte man nämlich die Bügel des Mittelstückes vertical zu
einander stellen, so würde man offenbar den Fehler verdoppeln, anstatt
paralysiren.
(gez.)
Friedr. Wilh. Blees.
II. Theorie des F. W. Blees'schen
Universal-Gelenkes; von dem kgl. Oberbergamts-Markscheider Rhodius in
Bonn.
Wir setzen (Tab. VI, Fig. 7) rechtwinkelige Coordinaten-Achsen voraus. Die Ebene in welcher
die Achsen OA und OB der beiden gekuppelten Wellen liegen, nehmen wir zur Ebene der x und y, die Halbirungslinie X'X des von den Achsen OA und OB
eingeschlossenen Winkels AOB zur Achse der x, den Punkt O zum Ursprung
der Coordinaten und OX zur positiven Halbachse.
Dann ist die Gleichung der Ebene, in welcher sich die Achse des Bolzens bewegt (wir
wollen dieselbe Bolzenebene nennen), die folgende:
1) y = 0.
Es sey der Winkel AOB durch
α bezeichnet, so sind die Gleichungen der
Achsen OA und OB
bezüglich.:
2) y = x
tang 1/2 α,
3) y = – x tang 1/2 α.
Die Gleichung einer beliebigen Ebene, welche durch den Ursprung der Coordinaten geht,
ist:
4) x + My + Nz = 0,
wo M und N reelle Coefficienten sind. Die Gleichung der Durchschnittslinie dieser
Ebene mit der Ebene der x und y wird erhalten, wenn man in 4) z = 0 setzt.
Dann erhält man aber x + My = 0 oder
5) y = – 1/M x.
Soll diese Gleichung die Linie OA ausdrücken, so muß sie mit der Gleichung 2) identisch seyn; man muß
also haben: – 1/M = tang 1/2 oder
6) M = – 1/tang 1/2 α = – cotang 1/2 α.
Soll aber die Gleichung 5) die Linie OB ausdrücken,
so muß sie mit der Gleichung 3) identisch seyn; es muß also dann seyn: –
1/M = – tang 1/2
α oder
7) M = cotang 1/2 α.
Substituirt man die gefundenen Werthe für M nach einander
aus 6) und 7) in die Gleichung 4), so erhält man die Gleichungen zweier Ebenen,
welche die Ebene der x und y
bezüglich in den Linien OA und OB schneiden. Der Coefficient N bleibt dabei, so lange weitere Bedingungen über die
Lage der beiden Ebenen nicht gegeben sind, unbestimmt. Wir wollen, um anzudeuten daß
wir den Cofficienten von z in der einen dieser
Gleichungen uns noch unabhängig von dem Coefficienten von z in der anderen dieser Gleichungen denken, in der einen N', in der anderen N'' statt
N setzen. Diese Gleichungen sind dann:
8) x – y cotang 1/2 α + N'z = 0,
9) x + y
cotang 1/2 α + N''z = 0.
Lassen wir N' und N'' ganz unbestimmt, so stellt die Gleichung 8) eine um die Achse OA, die Gleichung 9) eine um die Achse OB bewegliche Ebene, jede in beliebiger, von der
Lage der anderen unabhängiger Lage vor. Jedem bestimmten Werthe von N' oder N'' aber entspricht
eine bestimmte Neigung der einen oder der anderen dieser Ebenen gegen die Ebene der
x und y, welche zugleich
die Ebene des Winkels AOB ist.
Will man die Durchschnittslinien der Ebenen 8) und 9) mit der Bolzenebene haben, so
braucht man nur in den Gleichungen 8) und 9) nach Gleichung 1) (Gleichung der
Bolzenebene) y = 0 zu setzen. Dadurch erhält man:
10) x + N'z = 0,
11) x + N''z = 0.
Sollen die durch diese Gleichung ausgedrückten
Durchschnittslinien während der Rotation der Ebenen 8) und 9) um die Achsen OA und OB zu
jeder Zeit in eine Linie zusammenfallen, wie bei dem in Rede stehenden
Universal-Gelenk, wo die Bolzenachse diese Linie ist, so müssen die Gleichungen 10)
und 11) identisch seyn, d.h. es muß zu jeder Zeit seyn:
12) N' = N''.
Die Gleichungen 8) und 9) sind dann, wenn wir wieder N statt N' und N'' setzen, weil die Coefficienten von z in beiden Gleichungen nun nicht mehr von einander
unabhängig, sondern einander gleich sind:
8') x – y cotang 1/2 α + Nz = 0, 9') x + y cotang 1/2α + Nz = 0
Setzt man in der Gleichung 8') x =
x₁, y = y₁, in der Gleichung 9') x = x₁, y =
– y₁, so erhält man zwei identische
Gleichungen, welche also gleiche Werthe für z geben.
Zwei Punkte P und Q, von
denen der erste in der Ebene 8') liegt und die Coordinaten x₁ und y₁ hat, der andere in der
Ebene 9') sich befindet und die Coordinaten x₁
und – y₁ hat, haben daher gleiche Abstände
von der Ebene der x und y.
Die Coordinaten ihrer Projectionen auf diese Ebene sind bezüglich x₁, y₁ und x₁, – y₁. Diese Projectionen haben, wie ohne Weiteres erhellt, bezüglich
gleiche Abstände von den Achsen OA und OB. Es folgt hieraus, daß die Ebenen 8') und 9')
zu jeder Zeit gleiche Winkel mit der Ebene der x und y, d. i. mit der Ebene des Winkels AOB einschließen. Daraus aber folgt, daß die
Ebenen 8') und 9') zu jeder Zeit gleiche Rotationsgeschwindigkeiten bezüglich um die
Achsen OA und OB
haben, mögen diese Geschwindigkeiten an sich nun constant oder veränderlich
seyn.
Es ist nebenbei interessant, die Beziehung zu kennen, welche zwischen der
Rotationsgeschwindigkeit der Ebenen 8') und 9') und der Rotationsgeschwindigkeit des Bolzens besteht. Die
Gleichung der Bolzenachse ist nach 10) oder 11):
13) x + Nz = 0.
Es sey P irgend ein Punkt der Bolzenachse. Am Ende der
Zeit t sey ein Perpendikel vom Punkt P auf die Ebene der x und
y gefällt, und es sey E
der Fußpunkt dieses Perpendikels. Ist φ der
Winkel, den die Bolzenachse OP mit der Ebene der
x und y einschließt, so
ist cos φ = OE/OP, sin φ = PE/OP.
Fällt man von dem Punkte E die Perpendikel EF und EG auf
die Achsen OA und OB, so ist, wenn β den Neigungswinkel
der Ebenen 8') und 9') gegen die Ebene der x und y am Ende der Zeit t
vorstellt: EF = EG = PE . cotang
β, EF = EG = OE . sin 1/2 α, und
folglich:
PE . cotang β = OE . sin 1/2 α, oder OP . sin φ . cotang
β = OP . cos
φ . sin 1/2 α, oder:
14) tang φ = sin 1/2 α. tang
β.
Dieselbe Gleichung findet statt, wenn der Fußpunkt des von P auf die Ebene der x und
y gefällten Perpendikels auf die Halbachse OX', etwa in den Punkt E', fällt, in welchem Falle die Winkel β und φφ stumpf sind,
wenn sie in dem zuerst betrachteten Falle spitz waren.
Durch Differentiation der Gleichung 14) nach der Zeit t
erhält man, wenn jetzt die den Winkeln φ und β zugehörigen Bogen für den Halbmesser = 1 unter
φ und β
verstanden werden, 1/(cos φ)² . dφ/dt = sin 1/2 α . 1/(cos
β)² . dβ/dt und daher dφ/dt = sin
1/2 α.(cos
φ)²/(cos β)² . dβ/dt oder, wenn man
für
Textabbildung Bd. 176, S. 429
seinen aus 14) sich ergebenden Werth setzt,
Textabbildung Bd. 176, S. 429
Die Differentialquotienten dφ/dt und dβ/dt drücken die am Ende der Zeit t stattfindenden Winkelgeschwindigkeiten
(Rotationsgeschwindigkeiten) bezüglich des Kuppelungsbolzens und der um die Achsen
OA und OB
rotirenden Ebenen aus, und die Gleichung 15) gibt die Beziehung zwischen diesen
Winkelgeschwindigkeiten am Ende der beliebig gedachten Zeit t, also allgemein für jeden beliebigen Zeitmoment, unter der Bedingung, daß β den Bogen (für den Halbmesser = 1) des diesem
Zeitmoment entsprechenden Neigungswinkels der Ebenen 8') und 9') gegen die Ebene der
x und y vorstellt.
Ist die Rotationsgeschwindigkeit dβ/dt der Ebenen
8') und 9') constant, so findet ein Maximum oder ein Minimum der
Winkelgeschwindigkeit des dφ/dt des
Kuppelungsbolzens statt, wenn der Differentialquotient
Textabbildung Bd. 176, S. 430
der Null gleich wird, d. i. wenn
16) [(sin 1/2 α)² – 1] sin
β . cos β = 0
ist. Diese Gleichung kann aber, wenn nicht gerade (sin 1/2α)²
– 1 = 0, nur dann bestehen, wenn sin β. cos
β = 0, wenn also entweder cos β =
0 oder sin β = 0 ist. Im ersten Falle ist β = 1/2 π oder
β = 3/2 π,
im zweiten. Falle aber β = 0 oder β = π. Man,
sieht, daß während eines Umganges des Bolzens zweimal abwechselnd ein Maximum und
ein Minimum der Geschwindigkeit(dφ/dt) eintreten
muß. Das Maximum muß eintreten, wenn
Textabbildung Bd. 176, S. 430
negativ ist, das Minimum, wenn dieser Ausdruck positiv ist.
Man braucht aber, um zu erfahren, bei welchen der für β gefundenen Werthe Maxima und bei welchen dieser Werthe Minima der
Geschwindigkeit dφ/dt stattfinden, nicht einmal
zu untersuchen, ob
Textabbildung Bd. 176, S. 430
negativ oder positiv ist, man ersieht dieses schon ohne
Weiteres aus der Gleichung 15). Dieselbe zeigt nämlich, daß, da für β = 1/2 π und
für β = 3/2 π
die Werthe von dφ/dt entweder Maxima oder Minima
sind, bei diesen Werthen von β die
Geschwindigkeit dφ/dt jedesmal ein Maximum seyn
muß. Es folgt null schon von selbst, daß für β =
0 und für β = π die Minima von dφ/dt eintreten
müssen. Man sieht dieses aber auch direct ein. Hiernach ist jedesmal das Maximum der
Geschwindigkeit dφ/dt
17) V' = 1/sin 1/2α . dβ/dt, das Minimum aber
18) V'' = sin 1/2α . dβ/dt,
wenn man das Maximum durch V', das Minimum durch V'' bezeichnet. Es ist hiernach noch
19) V' = V''/(sin 1/2α)².
In dem einzigen Falle, wo (sin 1/2α)² – 1 = 0 ist, wird der Werth des Winkels β durch die Gleichung 16) nicht bestimmt, d.h. es
findet dann kein durch den Winkel β bedingtes
Maximum oder Minimum der Geschwindigkeit dφ/dt
statt. In diesem Falle hat man aber (sin 1/2α)² = 1, also 1/2 α = 90° und α =
180°. Die Achsen OA und OB liegen also dann in einer geraden Linie. Die Gleichung 15) gibt jetzt
dφ/dt = dβ/dt; also die Umdrehungsgeschwindigkeit des Kuppelungsbolzens
gleich der Rotationsgeschwindigkeit der gekuppelten Wellen, wie es in diesem Falle
nicht anders seyn kann.
Bonn, 8. Januar 1865.
gez. Rhodius.
Tafeln