| Titel: | Zwei neue Kuppelungen; von C. Reimann. |
| Autor: | C. Reimann |
| Fundstelle: | Band 188, Jahrgang 1868, Nr. CVII., S. 452 |
| Download: | XML |
CVII.
Zwei neue Kuppelungen; von C. Reimann.
Mit Abbildungen auf Tab.
VIII.
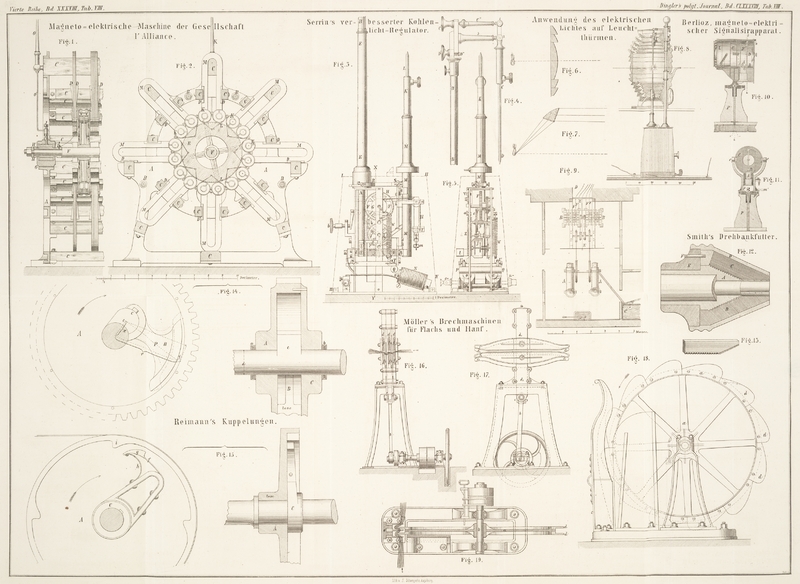
Reimann's Kuppelungen.
Die in Fig. 14
abgebildete Kraftmaschinen-Kuppelung besteht aus einem gußeisernen Kranze A, welcher auf der Welle d,
die von der Hülfsmaschine getrieben wird, zwischen zwei Frictionsringen a und b sich drehen kann;
außen ist der Ring mit Zähnen versehen, in die ein Stirnrad des Hauptmotors (z. B.
Wasserrad) eingreift. Die Welle d trägt eine Kurbel e, welche an ihrem Ende, um e als Achse, cylindrisch geformt ist, damit sich um diesen Theil der
Bremsschuh B wie um einen Zapfen bewegen kann. Dieser
Bremsschuh ist aus Gußeisen und an der Außenseite abgedreht, oder auch dort mit
Holzklötzen, am besten Eichenholz, garnirt. Damit der Schuh B sich nicht von der Kurbel entfernen kann, trägt diese bei c eine Nase, welche in einem Schlitze oder in einer
Aussparung sich bewegen kann. Vorn ist die Kuppelung geschlossen durch einen
gußeisernen Deckel C, der den Bremsschuh verhindert
herauszufallen und zugleich den Staub von den inneren Theilen der Kuppelung
abhält.
Läuft das Wasserrad, also auch der Kranz A schneller als
die Hülfsmaschine, so bleibt die Kurbel e relativ zum
Bremskranz A zurück: die Kuppelung ist ausgelöst; häufen
sich die Widerstände, so wird der Kranz A nach und nach
langsamer laufen, bis endlich d und mit ihr e schneller als A läuft,
dann wird sich die Kuppelung einkuppeln.
Ist M das Moment mit dem die Welle d getrieben wird, so tritt es mit der Kraft P
am Arm x in's Gleichgewicht, also M = Px, wo x die
Entfernung der Wellenachse vom Mittelpunkt e ist. Die
Kraft p, welche normal auf x
in e steht, preßt den Schuh B gegen den Kranz und ruft hier eine Reibung: μ P sin α hervor; μ der Reibungscoefficient.
Die andere Componente von P ist die Kraft P cos α, diese bemüht sich den Bremsschuh am
Kranze hinzuschieben; so lange nun
Textabbildung Bd. 188, S. 452
ist, so lange wird kein Gleiten des Schuhes eintreten,
folglich haben wir die Bedingung
Textabbildung Bd. 188, S. 452
Nehmen wir nach Morin für Gußeisen auf Gußeisen, wenig fettig,
μ = 0,15, so wird Textabbildung Bd. 188, S. 452 zu nehmen seyn, nehmen wir μ = 0,49, Eichenholz auf Gußeisen, so
wird Textabbildung Bd. 188, S. 453 zu nehmen seyn. Es ist gut diesen Winkel nicht größer als gerade
nothwendig ist zu machen, da es sonst leicht vorkommt, daß die Kuppelung sich nicht
von selbst auslöst, sondern festklemmt.
Wählen wir die Länge x = d,
wo d der berechnete Wellendurchmesser ist, so haben wir
zur Berechnung des Kranzes A folgende Gleichung:
Textabbildung Bd. 188, S. 453
Textabbildung Bd. 188, S. 453
Nehmen wir d als Einheit an, so
erhalten wir für unseren ersten Fall: r =6 d, für den zweiten: r = 2,3
d. Mittelst dieser Gleichungen kann man die
Kuppelung vergrößern oder verkleinern.
Diese Kuppelung hat den Vortheil der viel größeren Einfachheit und daher Billigkeit
vor den Kuppelungen von Uhlhorn und Pouyer-Quertier voraus; bei ihr sind die Gesperre dieser beiden
Kuppelungen vermieden, damit auch zugleich ihre Uebelstände.
Die zweite in Fig.
15 dargestellte Kuppelung erfüllt denselben Zweck wie die erste, nur ist
hier ein stummes Gesperre angewendet. A ist hier eine
Riemenscheibe, welche nach innen vier Vorsprünge hat, und welche lose auf der Welle
zwischen einem Anlauf und der festgekeilten Kurbel sich bewegen kann. Die Kurbel
trägt die Sperrklinke g an einer Stahlfeder f, welche beim Voreilen von A ein Zurückdrücken der Sperrklinke gestattet, beim Voreilen von C die Riemenscheibe mittelst Klinke und Sperrzahn i mitnimmt. Die Stahlfeder h
hat nur den Zweck die Sperrklinke daran zu verhindern gegen die Riemenscheibe zu
schlagen, sie macht also das Gesperr zu einem stummen. Obgleich diese zweite
Kuppelung den Eindruck macht, als ob mit ihr nur kleine Kräfte zu übertragen möglich
wäre, so zeigt die Rechnung doch das Gegentheil. Wäre z. B. die Welle 80 Millimet.
stark und die Kurbel 240 Millimet. lang, so wäre der Feder f ein Querschnitt von 45 Quadrat-Millimeter zu geben, also bei 1
Millimet. Stärke eine Breite von 45 Millimet.; will man die Feder noch schwächer
haben, so braucht man nur die Kurbel zu verlängern. Vorstehende Werthe sind auf
folgende Weise gefunden: Nimmt man mit Reuleaux das
Moment, welches durch eine 80 Millimeter starke Welle übertragen werden kann, zu
140780 Kil.-Millimet. an, so hält diesem Moment eine Kraft von 586,5 Kilogr.
an einem Arm von 240
Millimet. Länge das Gleichgewicht; es wird also durch die Feder f ein Zug von 586,5 Kilogr. zu übertragen seyn. Der
Zugtragmodul ist für ungehärteten Gußstahl 30, für gehärteten und angelassenen
Gußstahl 65–150; nehmen wir ihn zu 13 an, was einer Belastung, die auf Zug
wirkt, von 18000 Pfd. per Quadratzoll entspricht, so
erhalten wir einen Querschnitt von 45 Quadrat-Millimeter als den der Last
entsprechenden.
Berlin, im März 1868.
Tafeln