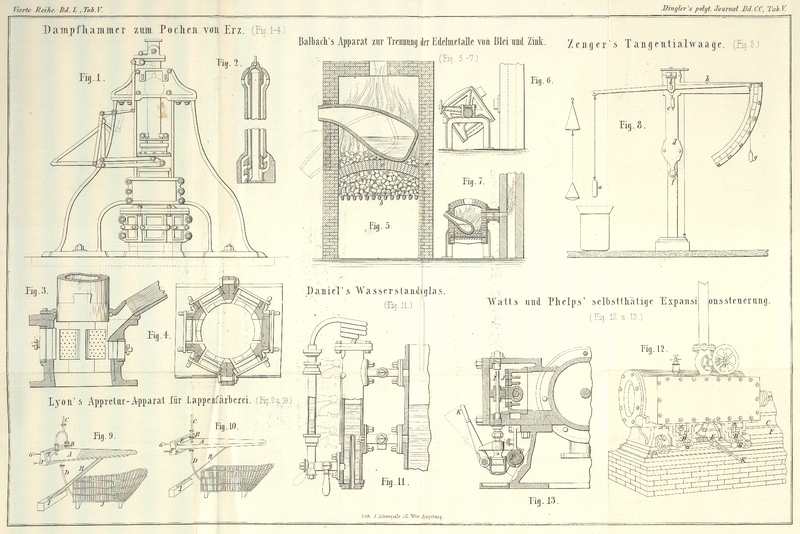
| Titel: | Professor Zenger's Tangentialwaage. |
| Autor: | Ferdinand Jicinsky |
| Fundstelle: | Band 200, Jahrgang 1871, Nr. XLIII., S. 161 |
| Download: | XML |
XLIII.
Professor Zenger's Tangentialwaage.
Mit theilweiser Benutzung der
Originalabhandlung mitgetheilt von Ferdinand Jicinsky.
Mit einer Abbildung auf Tab. V.
Zenger's Tangentialwaage.
Ich erlaube mir im Folgenden die Einrichtung und Anwendung einer
neuen Waage zu beschreiben, welche zufolge des in ihr
durchgeführten Principes das wissenschaftliche Interesse der
Physiker in hohem Grade erregen dürfte. Die einfache
Construction ferner und die Bequemlichkeit, Leichtigkeit und
Raschheit, mit welcher Dichtebestimmungen fester und flüssiger
Körper, genaue Bestimmungen hinsichtlich der
Ausdehnungscoefficienten für magnetische und elektrische
Spannungskräfte, ja selbst directe Wägungen an der
Tangentialwaage ausgeführt werden können, sichern derselben
nicht nur in wissenschaftlichen Cabineten, sondern auch in der
Praxis die ausgedehnteste Anwendung. Was speciell die
Dichtebestimmung anbelangt, wozu die Tangentialwaage am
häufigsten in der gesammten physikalischen und chemischen
Technik angewendet werden wird, so steht dieses Instrument von
den bis jetzt gebräuchlichen Saccharimetern und Senkspindeln
unerreicht da, indem selbst die empfindlichsten Saccharimeter
keine sehr genaue Ablesung darbieten (höchstens bis
0,05°), oft von geringfügigen Zufälligkeiten beeinflußt
werden und stets den Gebrauch ausgedehnter Nachschlagstabellen
bedingen.
Die von Hrn. Carl W. Zenger, Professor
der technischen Physik am böhmischen Polytechnicum zu Prag
construirte, der königl. böhmischen Gesellschaft der
Wissenschaften vorgelegte Tangentialwaage, welche in Fig. 8 dargestellt ist, besteht aus einer senkrechten
Leitstange mit einer Hülse d und dem
Bügel b, welcher an einer feinen
stählernen Achse in Achatlagern den 5zölligen leichten
Waagebalken mit dem auf- und abzuschraubenden
Cylindergewichtchen c trägt. Die
Hülse ist an der Leitstange vermöge des Griffes f mit Reibung beweglich. Der
Waagebalken trägt einerseits den Glaskörper a, oder, nach Bedarf, zwei
übereinander hängende Schälchen mittelst
Platindraht, andererseits ein Gewicht g und einen Zeiger, um hiermit den spiegelnd
versilberten Limbus von gleichfalls 5 Zoll zu bestreichen; h ist ein kleiner Stift, um das
vollständige Umkippen des Waagebalkens zu verhindern, da er
außer Gebrauch nicht horizontal im Gleichgewicht liegt.
Das ganze Instrument befindet sich im Glaskasten und ist mit zwei
Stellschrauben und dem Senkel einzustellen. Für
Dichtebestimmungen von Flüssigkeiten kommt der Glaskörper a in die zu prüfende Flüssigkeit;
bei Prüfung fester Körper ist derselbe durch die Waagschalen zu
ersetzen. Die Ablenkungswinkel am Limbus werden so abgelesen,
daß der Zeiger sein Spiegelbild deckt. Die Theilung gibt
unmittelbar einen halben Grad an, und mit Beihülfe einer Loupe
lassen sich noch die Zehntel davon, somit 1/20 eines Grades
abschätzen.
Textabbildung Bd. 200, S. 162
Ist nach vorstehender Figur abc
die horizontale Achse des Waagebalkens, und bezeichnen wir mit
c den Drehungspunkt, mit o und o'
den Schwerpunkt des ganzen Systemes, mit m das Gewicht des Waagebalkens, mit co = d die Tiefenentfernung des Schwerpunktes, mit p das Uebergewicht links und mit l die Länge des Waagebalkens, so ist
die Tangente des entstehenden Ablenkungswinkels (u) : tg
u = pl/md indem die Größe desselben
direct proportional ist dem Uebergewicht und verkehrt
proportional der Entfernung des Schwerpunktes und dem Gewichte
des Waagebalkens. Der Quotient l/md = k
bildet eine Constante, welche hauptsächlich von der Lage des
Schwerpunktes, nämlich von d
abhängig ist. Letzteres ist so zu wählen, daß k = l,
was durch das Cylinderchen c,
welches allein die Empfindlichkeit der Waage bestimmt, geschehen
kann.
Dem Gesagten zufolge transformirt sich die obige Gleichung auf
tg u = p. Mittelst des Cylindergewichtchens läßt sich die
Empfindlichkeit der Waage derart feststellen, daß die jeglichen
Gewichte den Tangenten der Ablenkungswinkel proportional sind,
und jedes Uebergewicht ist überdieß durch die Tangente seines
Ausschlages direct repräsentirt. Wäre z.B. der rechtsseitige
Waagebalken mit einer solchen Waagschale belastet, daß derselbe
in's Gleichgewicht käme und auf 45° zeigte, so wäre jede
Tangente der Ablenkungswinkel das absolute Gewicht für den
aufgelegten Körper, welches aus jeder Logarithmentafel direct zu
entnehmen ist. Für die geringen Gewichtsmengen, welche bei
chemischen Analysen zum Gebrauch dienen und die hiermit der
Empfindlichkeit der Waage vollkommen zu Statten kämen, ließe
sich das Gewicht von Körpern bis in die Centimilligramme genau
eruiren, so zu sagen momentan durch directes Ablesen, da der
Waagebalken keinen Schwankungen unterworfen ist und sogleich auf
die fragliche Ziffer trifft. Auf wie vielen von den
gebräuchlichen analytischen Waagen können wir uns bis in die
vierte Decimalstelle einlassen, und wie viel Glaubwürdigkeit
verdienen die Arbeiten jener Chemiker, welche von dem Schwindel
der Centimilligramme befangen sind?
1. Die
Dichtebestimmung von Flüssigkeiten mit der
Tangentialwaage.
Für Dichtebestimmungen von Flüssigkeiten ist die Waage durch den
Glaskörper a und das Gegengewicht
g so einzurichten, daß der
Waagebalken auf 0° einspielt, sobald das Glasstäbchen in
die specifisch leichteste Flüssigkeit eintaucht, z.B. in Aether
oder Alkohol. Der beim Eintauchen entstehende Gewichtsverlust
einerseits des Waagebalkens bringt diesen in's Gleichgewicht.
Bei einer derartigen Justirung können alle Flüssigkeiten, ob
schwerer oder leichter als Wasser, untersucht werden. Hat
Jemand, wie dieß z.B. in der Zuckerfabrication der Fall ist, nur
schwerere Flüssigkeiten als Wasser auf das specifische Gewicht
zu prüfen, so wird er zur bequemen Rechnung den Nullpunkt für
Wasser einstellen etc.
Für jede andere Flüssigkeit ist der Ablenkungswinkel ein anderer,
und da zur specifischen Gewichtsbestimmung nur das absolute
Gewicht eines gleichen Flüssigkeitsvolumens erforderlich ist und
die Gewichtsverluste thatsächlich andererseits am Waagebalken
belastend zur Wirkung gelangen, so ist für
die betreffende Dichte die Tangente des Ausschlages zur
Dichte der specifisch leichtesten Flüssigkeit
zuzuschlagen, nach der Formel d = d₀ + tg u, worin
d die fragliche Dichte, d₀ die Dichte der leichtesten
Flüssigkeit (z.B. Aether) und u den
Ablenkungswinkel bedeuten.Bezeichnen wir mit x das
Gewicht des Glasstäbchens sammt Platindraht, mit y den Gewichtsverlust in der
Flüssigkeit, mit m das
Gewicht des Waagebalkens, mit d den Abstand des Schwerpunktes von der
Umdrehungsachse, mit l die
Länge des Hebelarmes und mit u den Ablenkungswinkel, so ist in der vorigen
Gleichung tg u = p l/md das p durch den Ausdruck der nun
wirkenden Resultante (p +
y) – x zu ersetzen. Somit tg u = [(p + y) – x]
1/md (1.In derselben Weise ist der Ablenkungswinkel u₀ für Aethertg u₀ = [(p + y₀) – x] 1/md –
(2. Da der Ablenkungswinkel für Aether u₀ = 0 so muß p + y₀ = x oder
p – x – y₀
Bedingungsgleichung für das Gleichgewicht seyn.Wird eine specifisch schwerere Flüssigkeit als Aether
gemessen, so ist in die Gleichung Nr. 2 noch der
Ueberschuß (y₀) des
nun auftretenden Gewichtsverlustes in Rechnung zu
ziehen, und es ist tg u =
[p + y₀ + y₁ – x] 1/md. Für p + y₀ = x und 1/md = 1 ist tg u = y₁, d.h. die Tangente
des Ausschlages ist gleich dem Ueberschusse des
Gewichtsverlustes in der zu prüfenden Flüssigkeit gegen
jenen in Aether. Der gesammte Gewichtsverlust beziffert
sich mithin mit y = y₀ + y₁ = y₀ + tg u oder für die
Volumseinheit und mit Bezug auf die Dichten d = d₀ + tg u.
„Man findet somit die Dichte
einer Flüssigkeit mittelst der Tangentialwaage, wenn man
zu der Dichte der für die Waage angepaßten leichtesten
Flüssigkeit die Tangente des Ablenkungswinkels
addirt.“
Eine Ablenkung von 1° z.B. entspricht einer Dichte von d = 0,7300 + 0,0175 = 0,7475, worin
0,7300 die Dichte des Aethers und 0,0175 die Zunahme des
Gewichtsverlustes für 1° Ausschlag ist.
Bei einem Volum des Glasstäbchens von etwa 1 Kubikcentimeter geht
somit die Empfindlichkeit der Waage für 1° Ablenkung bis
17,5 Milligramme und bei Abschätzung von 1/20° bis
17,5/20 = 0,875 Milligramm, nahezu 1 Milligrm., was die genaue
Dichtebestimmung bis zur dritten Decimalstelle ermöglicht.
Zur Erleichterung der Rechnung hat Prof. Zenger die folgende Tabelle zusammengestellt. Sie
enthält die natürlichen Tangenten von halben zu halben Graden,
ferner in der Rubrik d die
entsprechenden Dichten von der des Aethers 0,736 bei 0°
C. beginnend, bis zur Dichte der concentrirtesten Schwefelsäure,
und unter ∆ 3' die
Differenzen für 1/20° = 3'.
Textabbildung Bd. 200, S. 165
Für einen Unterschied der Temperaturen ist die gefundene Dichte
nach der Tabelle auf die Normaltemperatur 0° C. zu
reduciren. Zur Temperaturbestimmung kann zweckmäßig ein kleines
Thermometer als Einsenkkörper dienen. Der kleine Fehler des
Resultates, welcher entsteht, wenn bei anderer Temperatur
geprüft wird, beruht nur in der Verschiedenheit der
Ausdehnungscoefficienten des Glases und der zu messenden
Flüssigkeiten. Wäre das Verhältniß der beiden
Ausdehnungscoefficienten gleich 1 oder überhaupt eine Constante,
so könnte die Temperatur bei der Untersuchung auch
unberücksichtigt bleiben.
Zum Schluß dieses Capitels sey uns nur noch gestattet, eine
kleine Vergleichstabelle der von Prof. Zenger mit dem Aräometer, dem Pyknometer und der
Tangentialwaage an verschiedenen Flüssigkeiten ausgeführten
interessanten Versuche zu recapituliren:
Temperatur
Ablenkungswinkel
tg
u
Dichte
Wasser
15°
C.
11°
35'
0,2049
0,9989
Alkohol 1)
16
1 25
0,0204
0,8144
Alkohol 2)
16
2 45
0,0466
0,8366
engl. Schwefelsäure
19
45
0
1,0000
1,7940
Temperatur
Meißner'sAräometer
Norm.Branntweinwaage
Pyknometer
Tangentialwaage
Wasser
15°
C.
0,999
–
–
0,9989
Alkohol 1)
16
0,812
0,815
0,815
0,8144
Alkohol 2)
16
0,835
0,838
0,839
0,8366
engl. Schwefelsäure
19
1,795
–
1,792
1,7940
Nimmt man die Mittel aus den Aräometer- und
Pyknometerbestimmungen, so ergibt sich:
Mittel
Tangentialwaage
Differenz
Wasser
0,9990
0,9989
– 0,0001
Alkohol 1)
0,8140
0,8144
+ 0,0004
Alkohol 2)
0,8373
0,8366
– 0,0007
engl.
Schwefelsäure
1,7935
1,7940
+ 0,0005
2. Bestimmung der
Dichten fester Körper mittelst der
Tangentialwaage.
Wie bereits bemerkt, ist hierzu die Doppelwaagschale und
destillirtes Wasser zu verwenden. Die Manipulation und
Berechnung befolgt dieselben mathematischen Principien und
Formeln.
Die Gewichtsprüfung kann im Ganzen nach drei Methoden vorgenommen
werden.
Erste Methode. – Wäre der
constante Winkel welchen die untere Waagschale durch
Gewichtsverlust beim Eintauchen in Wasser hervorbringt, u₁ und legen wir auf die
obere Waagschale so viel vom festen Körper, daß der Waagebalken
wieder zu 0° zurückkehrt, so ist tg u₁, das absolute Gewicht desselben.
Der feste Körper, in die untere Waagschale gebracht und in Wasser
getaucht, bringt natürlich einen anderen Winkel u hervor, dessen Tangente dem
absoluten Gewicht eines gleichen Wasservolumens entspricht. Nach
der bekannten Formel, welche die Dichte fester Körper durch das
Gewichtsverhältniß gleicher Volume vom festen Körper und Wasser
ausdrückt, ist die zu suchende Dichte D = tg u₁/tg u = tg
u₁ . cotg u.
„Man findet somit die Dichte
fester Körper durch Multiplication der Tangente des
Ausschlages für die Waagschale mit der Cotangente jenes
für den eingetauchten Körper.“
Ist
p das Gewicht der
Schälchen und Aufhängedrähte,
x der
Gewichtsverlust der unteren Schale,
p₁ das
Gewicht am anderen Hebelarme,
q das absolute
Gewicht des festen Körpers und
y sein
Gewichtsverlust im Wasser,
u der
Ablenkungswinkel für den festen Körper und
u₁ für die
Waagschale,
so haben wir in der Formel tg u = pl/md statt p nur die
im positiven Sinne wirtenden Kräfte p₁, x und die im negativen Sinne
wirkenden p und q mit plus oder minus
einzuführen und erhalten so tg
u₀ = (p₁ – p +
x – q) 1/md für den Ablenkungswinkel der Waagschale.
Für den Ablenkungswinkel des festen Körpers ist noch
dessen Gewichtsverlust im Wasser als positiv wirkend in
die Formel zu bringen; somit tg
u = = (p₁
– p + x – q + y) 1/md und da der feste Körper
den Waagebalken auf 0° zurückführt, muß tg u₀ = 0, oder (in
der ersten Formel) (p₁ – p +
x – q) = 0. Wornach das Gewicht
des festen Körpers q = p₁ – p + x und die Gleichung 2) übergeht in tg u = yl/md = y. Ebenso ist
die Formel für die eingetauchte Waagschale abzuleiten:
tg u₁ = (p₁ – p + x) l/md = ql/md = q; und die Dichte resultirt
aus dem Verhältniß D = q/y = tg
u₁/tg u =
tg u₁ cotg u.
Offenbar ist für diese Prüfungsmethode tg
u₁ eine Constante. Prof. Zenger berechnete hiermit eine Tabelle, welche die
Cotangenten für einzelne Grade bis 50° mit obiger
Konstante q = 0,3443 und q¹ = 1,1918 multiplicirt
enthält. Die Dichten sind übrigens direct aus der Tabelle zu
entnehmen. Sind Körper von sehr großer Dichte zu prüfen, so wird
diese Methode etwas ungenau, da das verdrängte Wasservolumen und
der diesem entsprechende Ablenkungswinkel für den eingetauchten
Körper unbedeutend sind. In diesem Falle gibt man der
unbelasteten Waage ein Auflegegewicht für den Ablenkungswinkel
von 50° am Limbus, und sind die Dichten dann in der
zweiten Tabelle mit q = 1,1918 = tg 50° aufzusuchen.
Tabelle zur Messung der
Dichte fester Körper.
q = 0,3443
q = 1,1918
u
cot
u
∆3'
Dichte
u₀
cot
u
∆3'
Dichte
0° 30' 1 0 1 30 2 0 3 0 4 0 5 0 6 0 7 0 8 0 9 010 011 012 013 014 015 016 017 018 019 020 021 022 023 0
114,59057,29038,18828,63619,08114,30111,4309,5148,1447,1156,3145,6715,1454,7054,3314,0113,7323,4873,2713,0782,9042,7472,6052,4752,356
1,9730,6580,1640,1640,0820,0490,0330,0240,0180,0140,1100,0090,0080,0070,0060,0050,0040,0040,0030,0030,0030,0020,0020,002
39,45319,72413,1489,8596,5704,9243,9353,2762,8042,4502,1741,9531,7871,6201,4911,3811,2851,2011,1261,0601,0000,9460,8970,8520,811
3° 4 5 6 7 8 9101112131415161718192021222324252627282930
19,08114,30111,4309,5148,1447,1156,3145,6715,1454,7054,3314,0113,7323,4873,2713,0782,9042,7472,6052,4752,3562,2462,1442,0501,9631,8811,8041,732
0,2860,1700,1140,0820,0610,0480,0380,0310,0260,0220,0190,0170,0150,0130,0120,0100,0090,0080,0080,0070,0050,0050,0050,0050,0050,0040,004
22,74017,02913,62511,3399,7068,4807,5256,7596,1315,6075,1624,7804,4484,1563,8993,6683,4633,2743,1042,9492,7782,6772,5562,4442,3392,2412,1502,064
Zweite Methode. – Die
Herstellung der Gleichgewichtslage durch jedesmaliges Auflegen
des festen Körpers wird, namentlich wenn derselbe in den
zweckentsprechenden kleinen Stücken schwer zu erlangen ist,
etwas zeitraubend. Man kann dann, ohne Rücksicht auf das
Zurückweichen des Waagebalkens auf den Nullpunkt, ein beliebiges
verfügbares Fragment verwenden, welches überhaupt noch eine
Abweichung im Gebiete des Limbus veranlaßt. Nur ist dann das
Gewicht auf die Tangente dieses neuen Ablenkungswinkels zu
beziehen und die Dichte auf diese neue Basis zurückzuführen. Die
längere Manipulation bei der ersten Methode ist bei der zweiten
durch eine complicirtere, aber doch raschere Rechnung ersetzt.
Statt mit einfachen Winkeln, hat man es in derselben mit
Winkeldifferenzen resp. mit dem Verhältniß der
Tangentendifferenzen zu thun.
Ist
v der
Ablenkungswinkel
der unbelasteten Waage,
u
„
„
bei Belastung (kleiner als v),
und
u₁ „
„
im Wasser am unteren Schälchen, so
ist das Gewicht des Körpers q = tg v
– tg u₁, das Gewicht
des Wasserkörpers z.B. s = tg u₁ – tg u und die Dichte D = (tg
v – tg
u₁)/(tg u₁
– tg u).
Dritte Methode. – Sie eignet
sich für Körper deren Dichte 10 übersteigt. Man legt zunächst
den Körper auf die obere Waagschale, hernach auf die untere,
tarnt ferner, nach vollständiger Beseitigung des Körpers, z.B.
mit Schrot aus und untersucht ebenso wie früher den
Gewichtsverlust der Tara durch Auflegen derselben auf die untere
Waagschale im Wasser.
Offenbar ist das Schrot ein Vergleichungskörper, auf dessen zu
untersuchende oder genau bekannte Dichte die Dichte des festen
Körpers vorläufig bezogen wird.
Bezeichnen wir
mit
u₀ den Winkel für
die belastete Waage,
„
u die
Ablenkung für den eingetauchten Körper, und mit
u₁ „ „
für die an der unteren Waagschale
eingetauchte Tara, so ist tg u₁ – tg u₀, der Gewichtsverlust
des zu untersuchenden Körpers im Wasser und tg u₁ – tg u₀ der Gewichtsverlust der
Tara, und die Dichte des Körpers D =
(tg u₁ – tg u₀)(/tg u – tg u₀) mit Bezug auf die gebrauchte Tara, oder
D = (tg
u₁ – tg
u₀)(/tg u – tg
u₀) D₁ mit
Bezug auf Wasser, worin D₁
die Dichte der Tara bedeutet.Die bezüglichen mathematischen Beweise sind nach der
früher mitgetheilten Schablone durchzuführen.
Die Justirung der Waage anbelangend, sey noch zum Schluß erwähnt,
daß man zuerst den Nullpunkt entweder für Aether oder absoluten
Alkohol feststellt und dann den Winkel für destillirtes Wasser
bei 4° C. und jenen für concentrirte Schwefelsäure von
genau bekannter Dichte berechnet und prüft, und nöthigenfalls
mit dem Cylindergewichtchen auf die richtige Stellung des
Waagebalkens nachhilft. Zur Winkelberechnung dient die Gleichung
tg u = d – d₀, wo
d₀ die Normaldichte und
d die Wasser- oder
Schwefelsäuredichte bedeuten.
Sind mit der Tangentialwaage Ausdehnungscoefficienten zu
berechnen, so erhitzt man die Flüssigkeit im Glas bis etwas über
die Temperatur bei welcher man beobachten will, und läßt dann
mit eingesenktem Thermometer an der Waage abkühlen. Aus dem
specifischen Gewichtsunterschied resultirt sogleich die Zunahme
für die Volumseinheit.
Die Wichtigkeit der Tangentialwaage für die Technik ist bereits
im Eingange hinreichend betont worden; wir erlauben uns noch
namentlich die Herren Interessenten für Zuckerfabrication auf
diese Waage aufmerksam zu machen, da dieselbe ein vortreffliches
Mittel zur Bestimmung des specifischen Gewichtes sämmtlicher
Säfte und Syrupe abgibt.Genaue Exemplare verfertigt für 50 fl. österr. Währ. Herr
Bozek,
Institutsmechaniker am böhmischen Polytechnicum zu
Prag.
Prag, im April 1871.
Tafeln